Let's Write a Train Tracking Algorithm
I delivered a 20-minute presentation on September 20th at iOSDC Japan 2025.
If you prefer video:
Other materials:
- GitHub: train-tracker-talk - Open source code and presentation materials
- Blog: I Presented At iOSDC 2025 - More about the conference and presentation context
- App Store: Eki Live - The app discussed in the presenation
This post is a deconstructed version of the talk with the slide images above and my speaker notes in English below.

- Lately I’ve been working on an app called Eki Live.
- Today I’m going to talk about a part of that app.
- So what do I mean by train tracking algorithm?
- Well, when riding a train, it’s useful to know the upcoming station.

- On the train, we can see the train information display or listen for announcements.
- But would it also be useful to see this information in your Dynamic Island?

- In my talk, we’ll first review the data prerequisites we’ll need for the algorithm.
- Then, we’ll write each part of the algorithm, improving it step-by-step.

- We need two types of data for the train tracking algorithm:
- Static data that describes the railway system of greater Tokyo.
- And Live GPS data from the iPhone user.
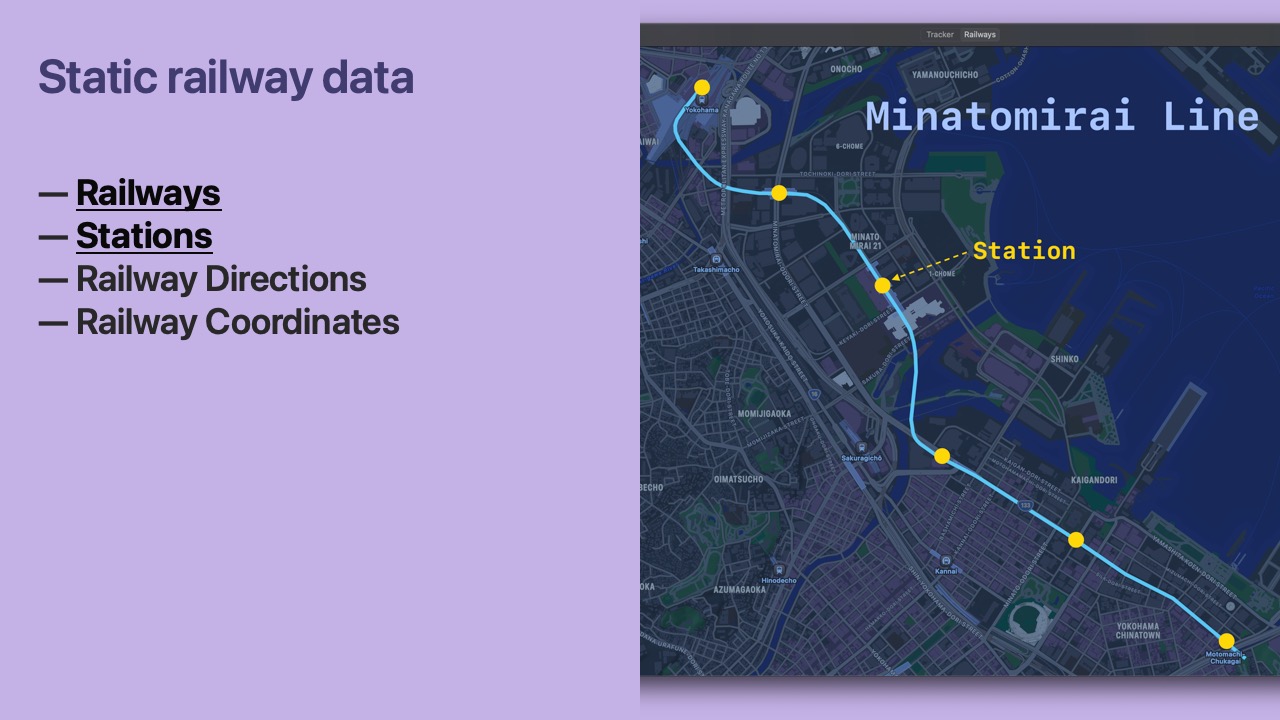
- Railways are ordered groups of Stations.
- In this example, we can see that the Minatomirai Line is made up of 6 stations.
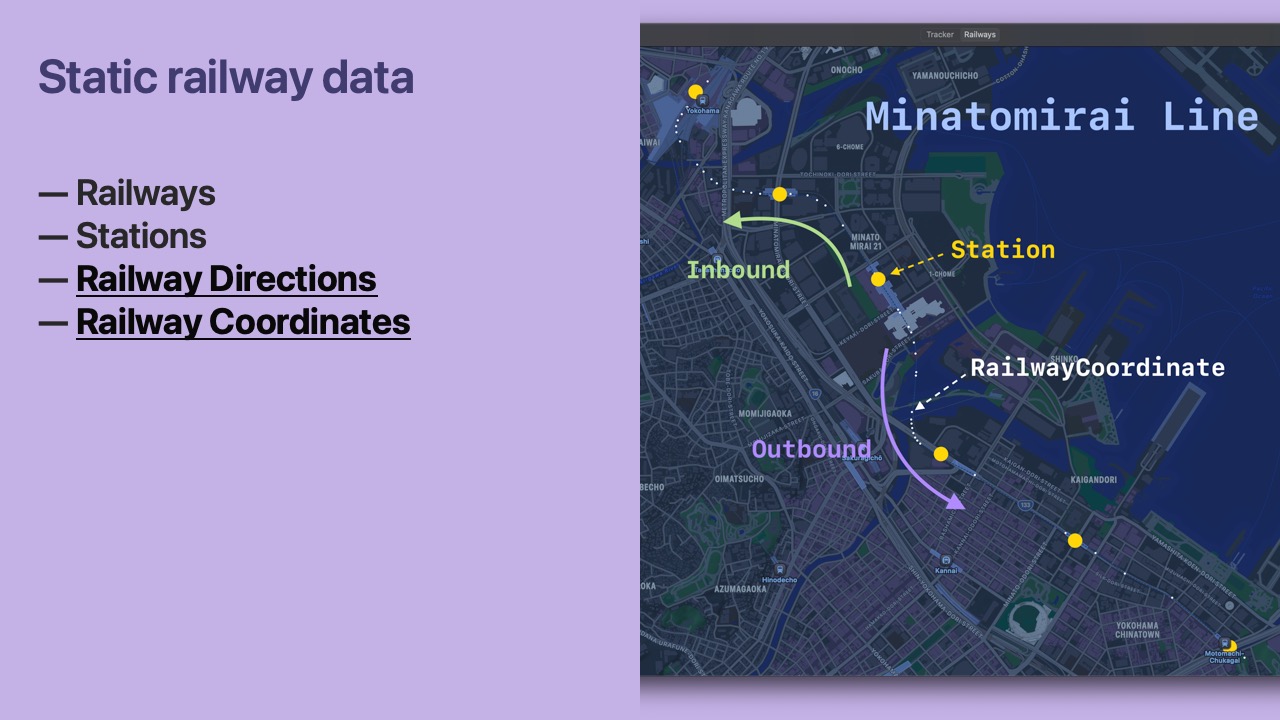
- Trains travel in both Directions on a Railway.
- Coordinates make up the path of a Railway’s physical tracks.
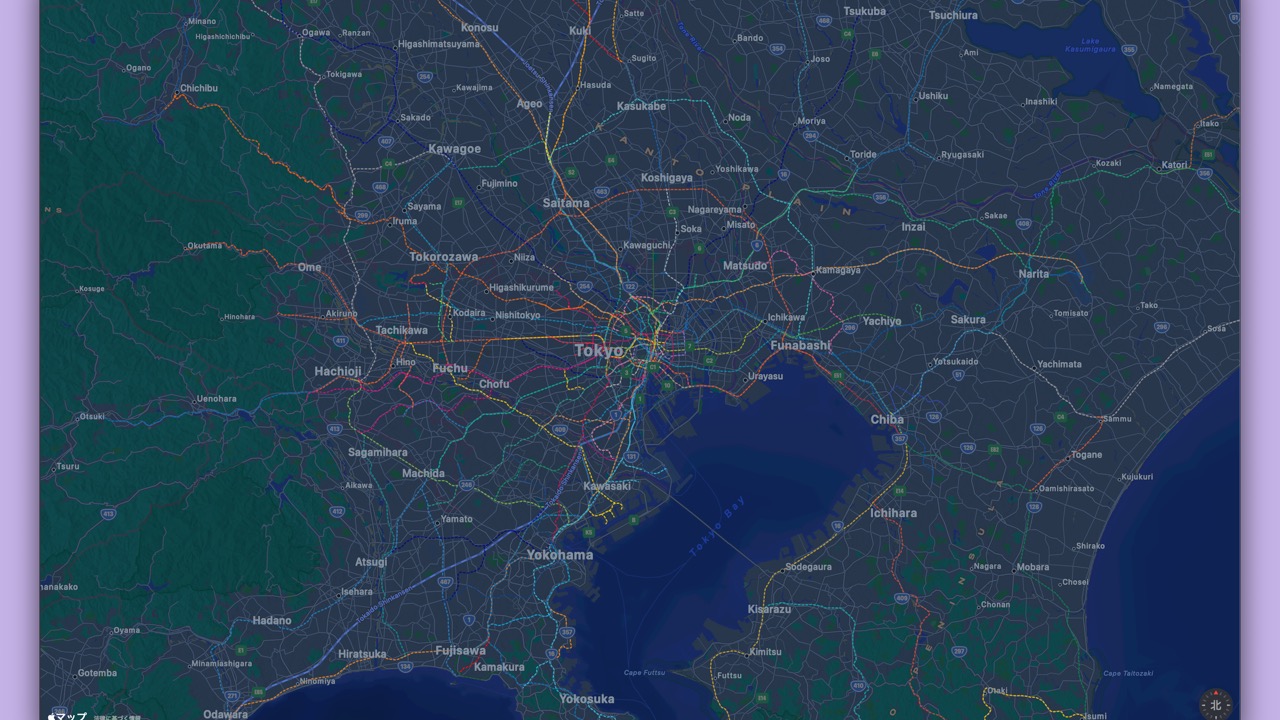
- This map shows the Railway data we’ll be using.
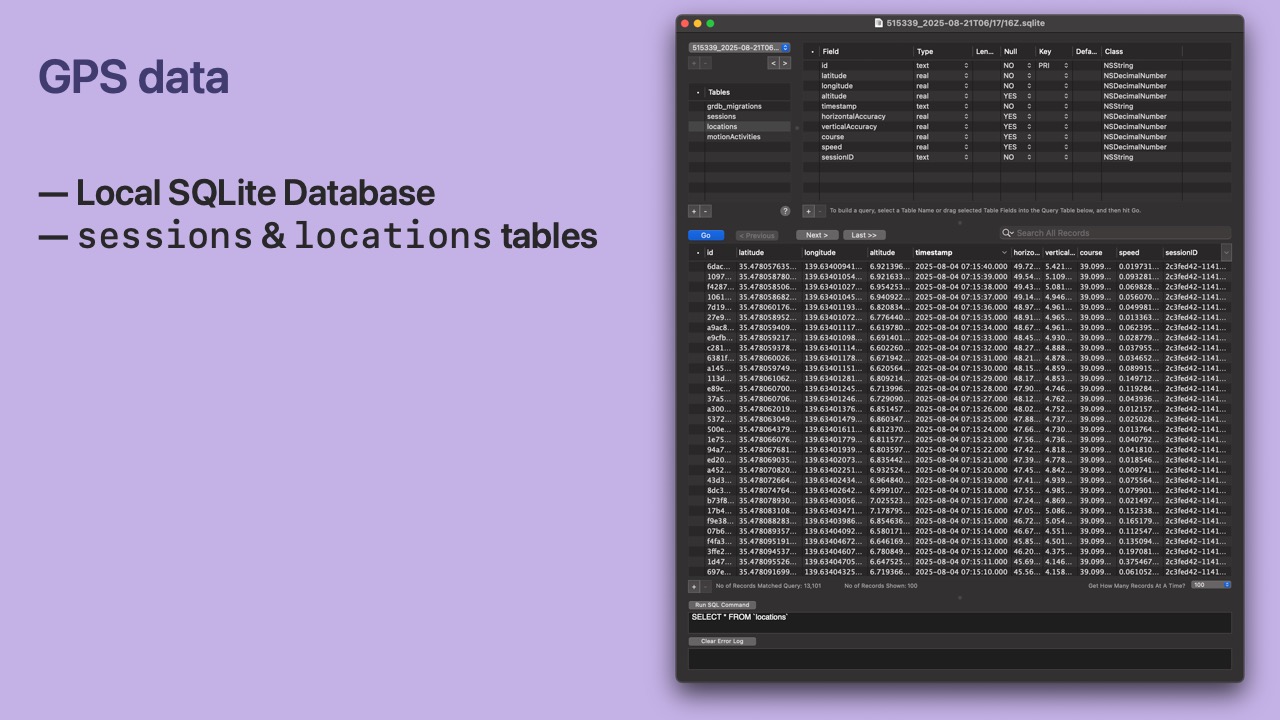
- We collect live GPS data from an iPhone using the Core Location framework.
- We store the data in a local SQLite database.
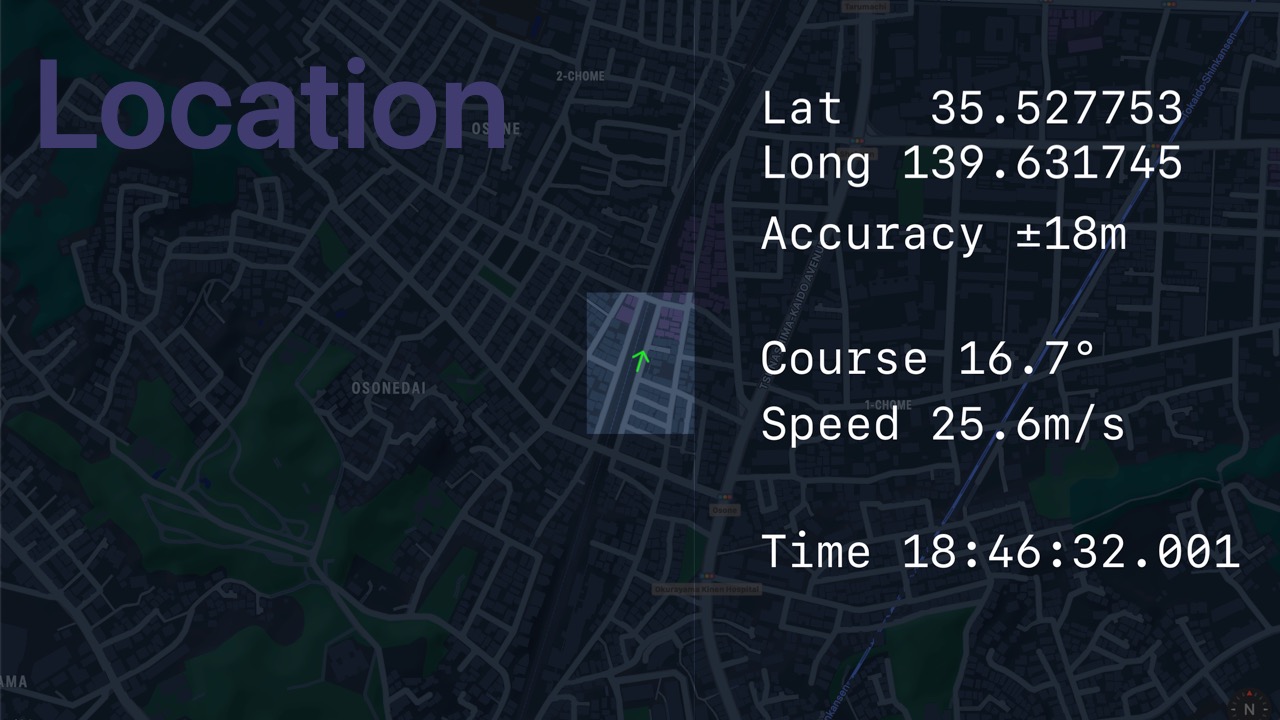
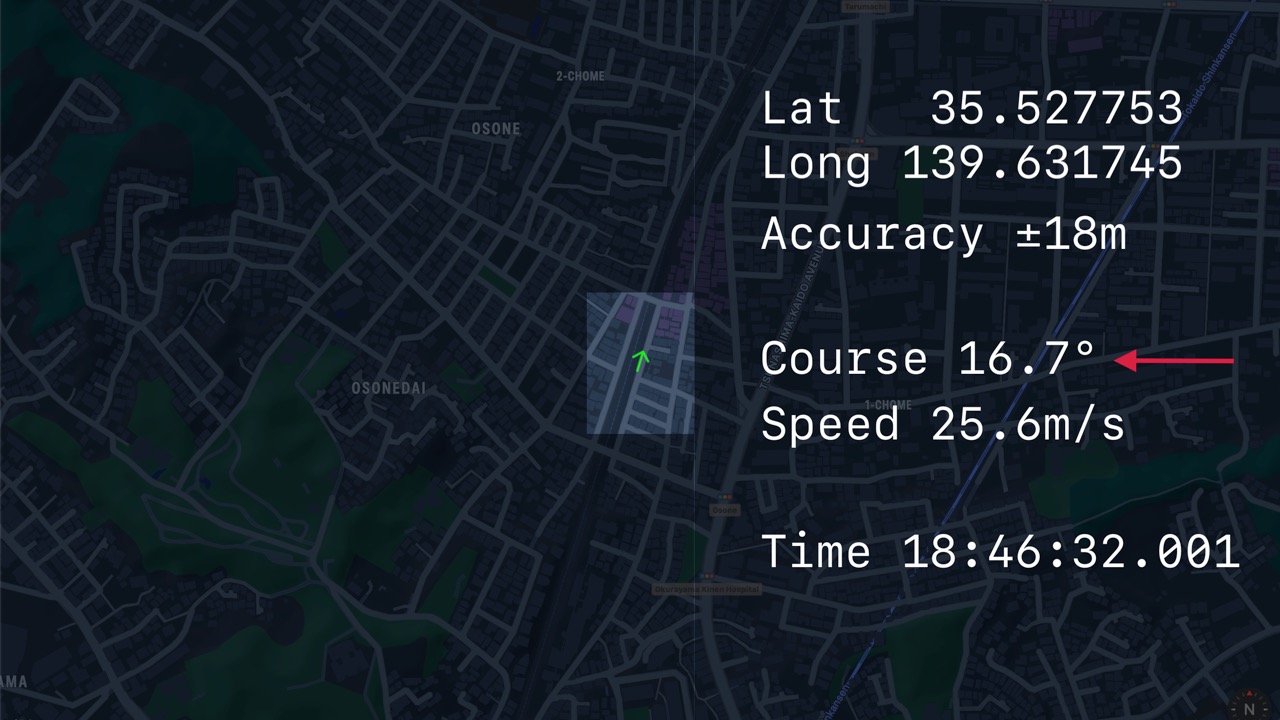
- A
Locationhas all data fromCLLocation. - Latitude, longitude, speed, course, accuracy, etc.
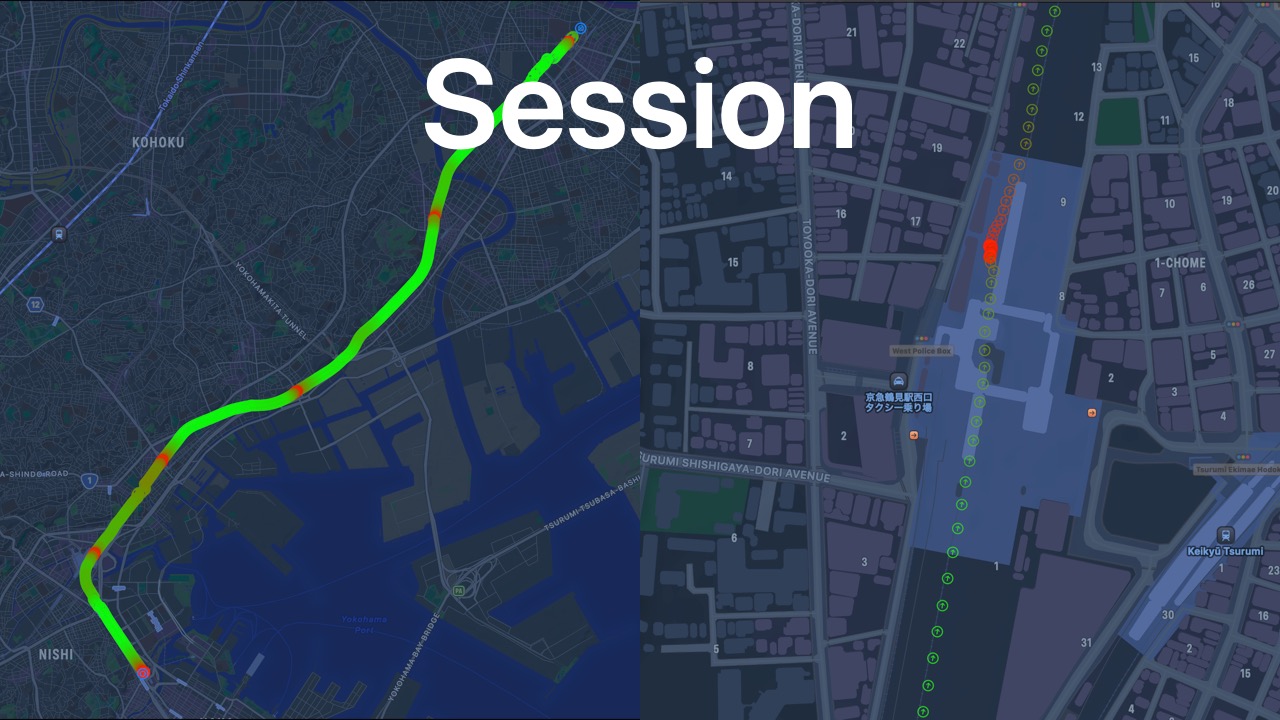
- A Session is an ordered list of Locations.
- A Session represents a possible journey.
- Green is for fast and red is for stopped.
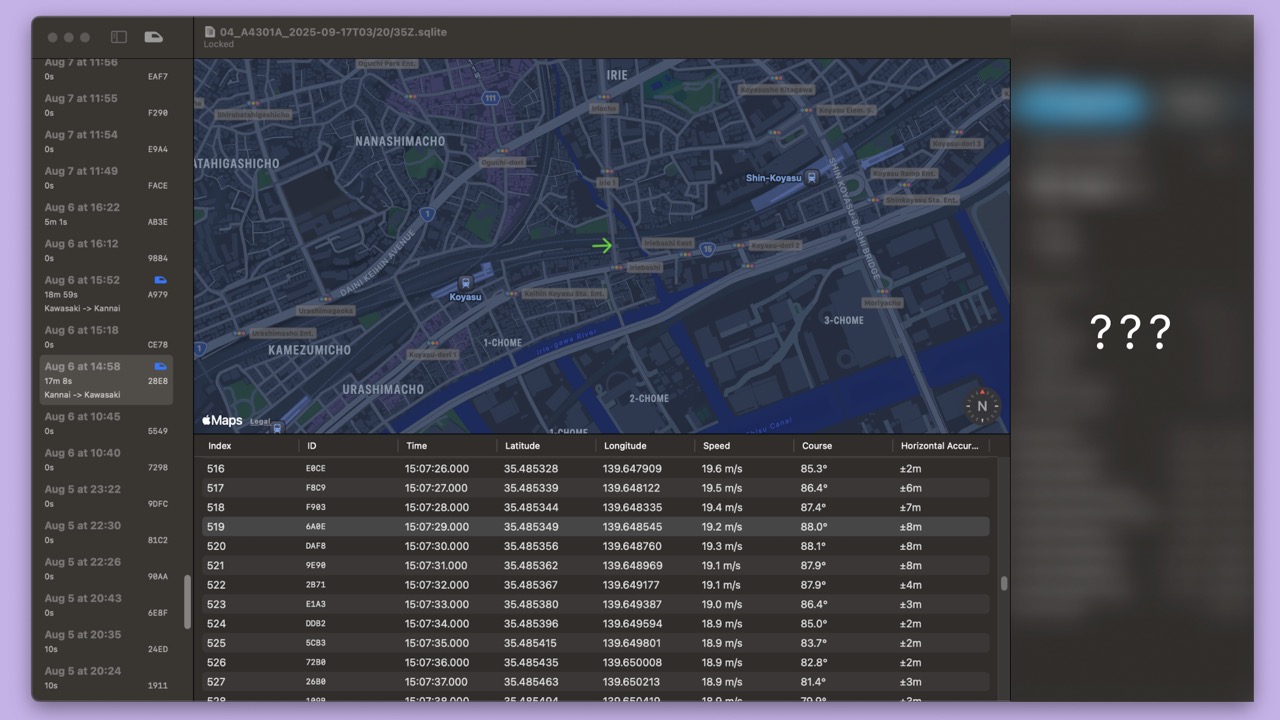
- I created a macOS app to visualize the raw data.
- In the left sidebar there is a list of Sessions.
- In the bottom panel there is a list of ordered Locations for a Session.
- Clicking on a Location shows its position and course on the map.

- Our goal is to write an algorithm that determines 3 types of information:
- The Railway, the direction of the train, and the next Station.
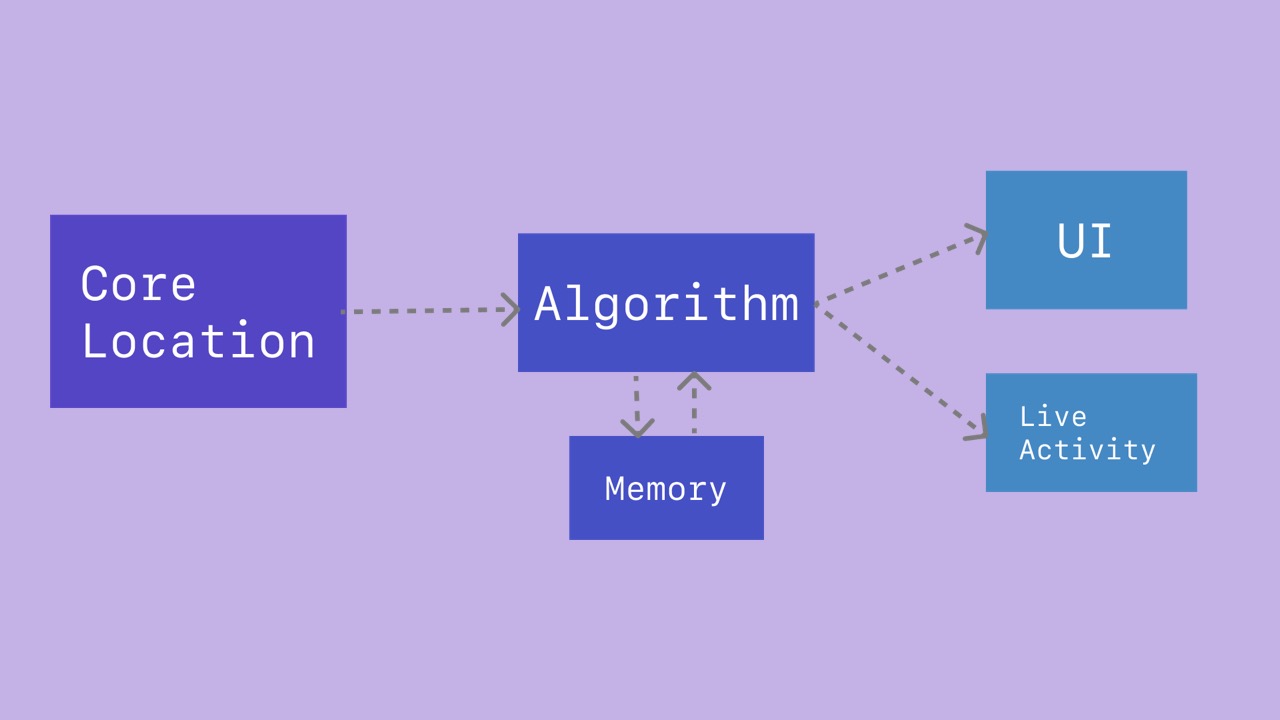
- Here is a brief overview of the system.
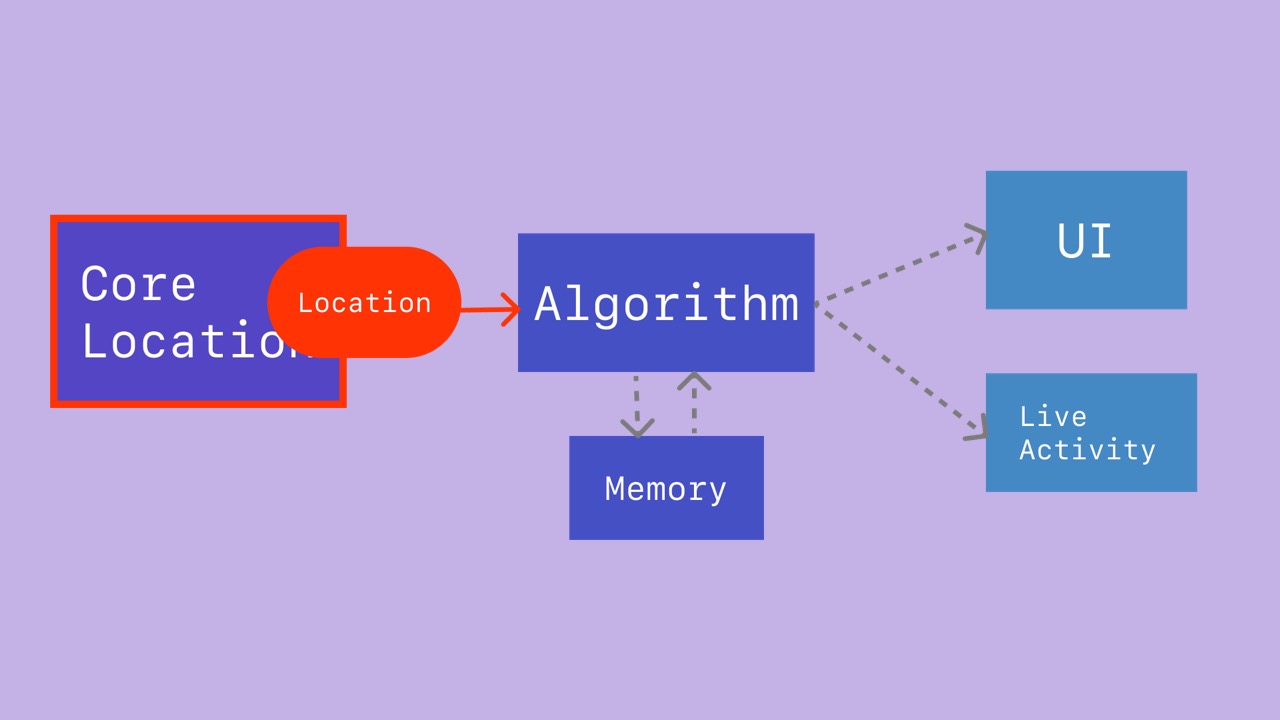
- The app channels
Locationvalues to the algorithm.
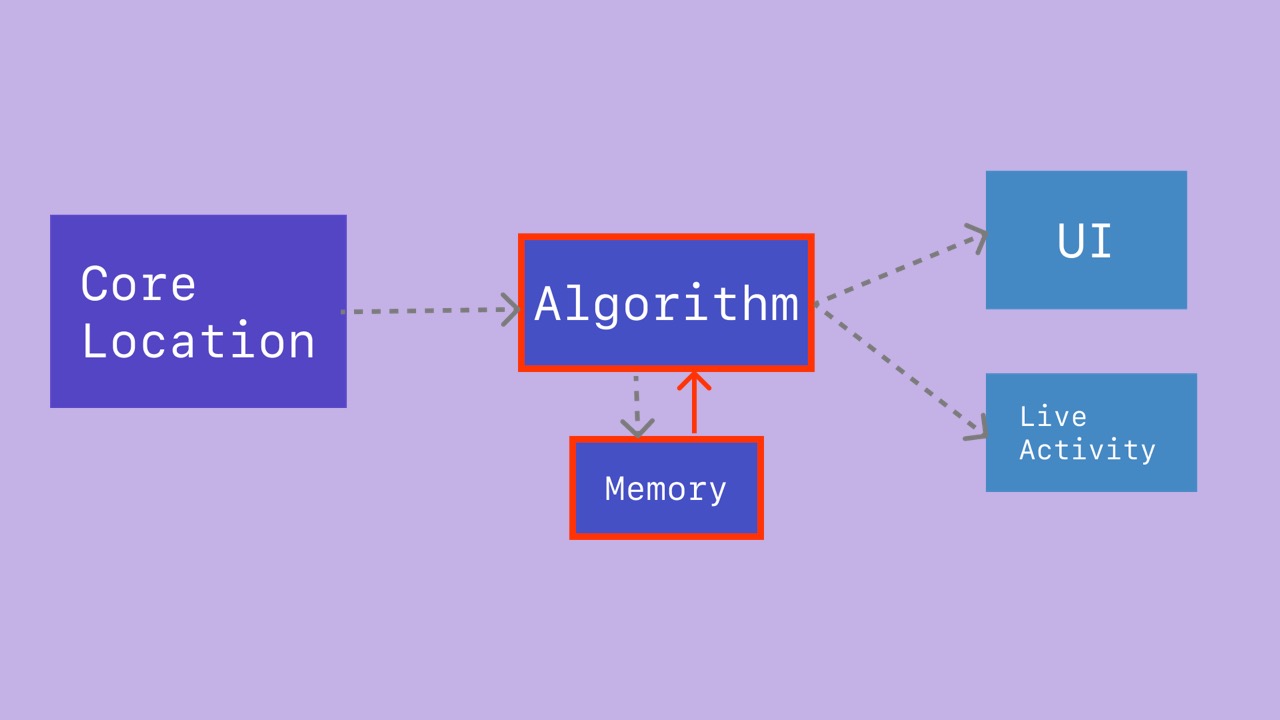
- The algorithm reads the
Locationand gathers information from its memory.
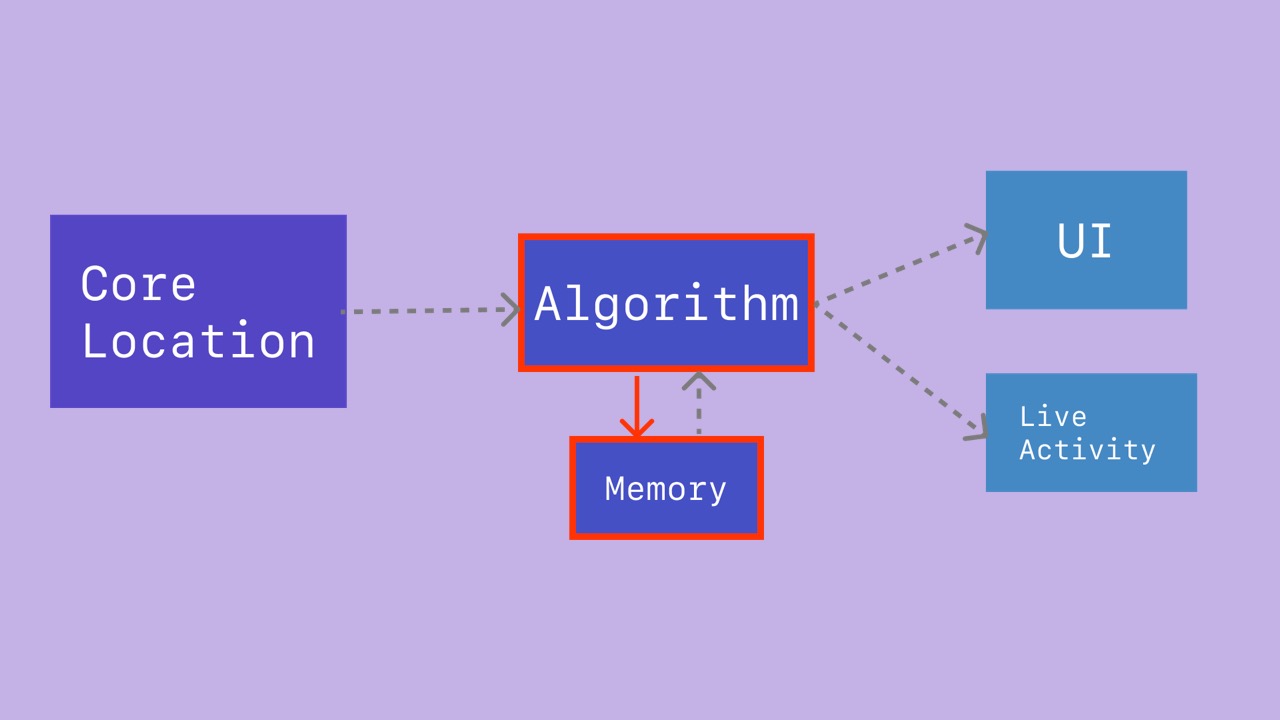
- The algorithm updates its understanding of the device’s location in the world.
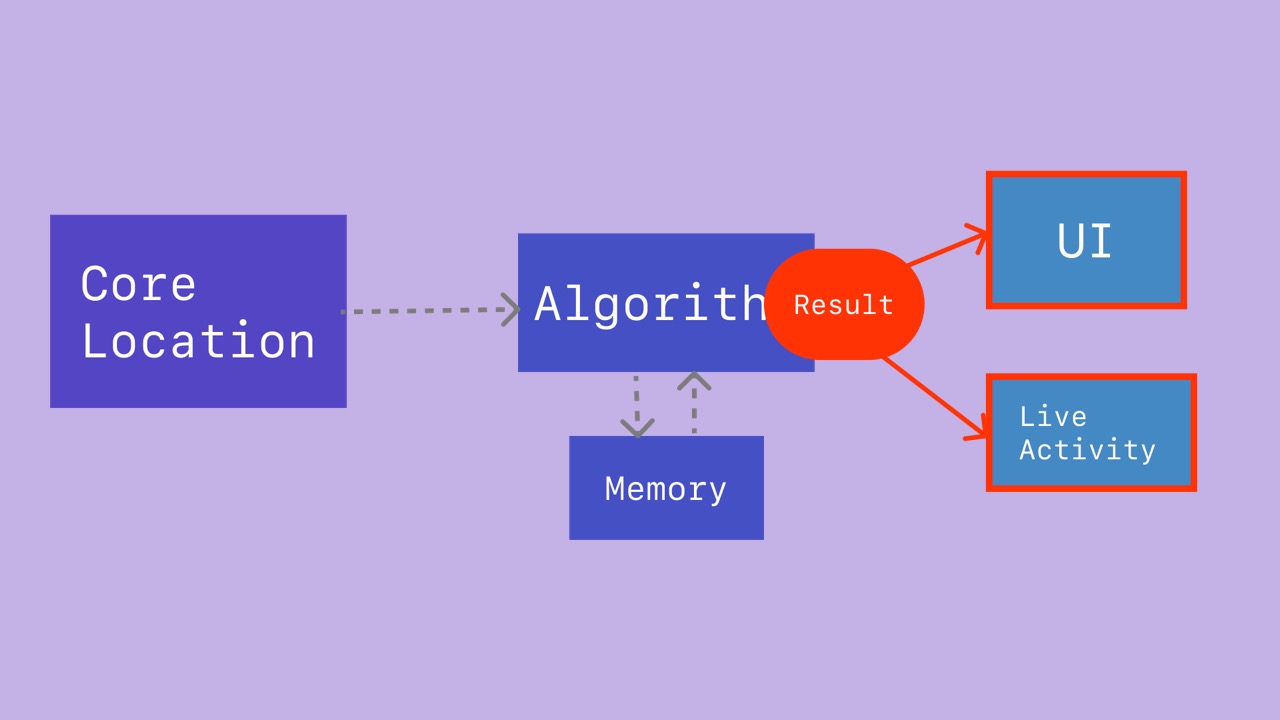
- The algorithm calculates a new result set of railway, direction, and station phase.
- The result is used to update the app UI and Live Activity.
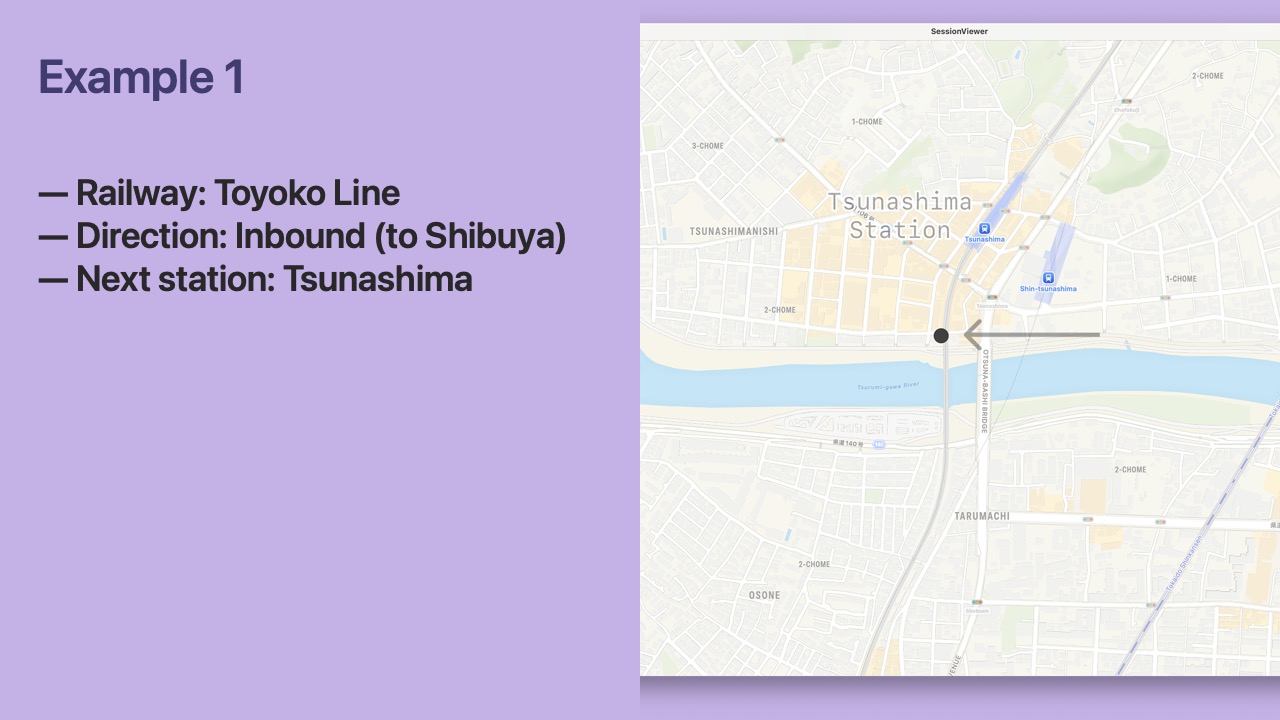
- Let’s start by considering a single
Location. - I captured this Location while riding the Tokyu Toyoko Line close to Tsunashima Station.

- Can we determine the Railway from just this Location?
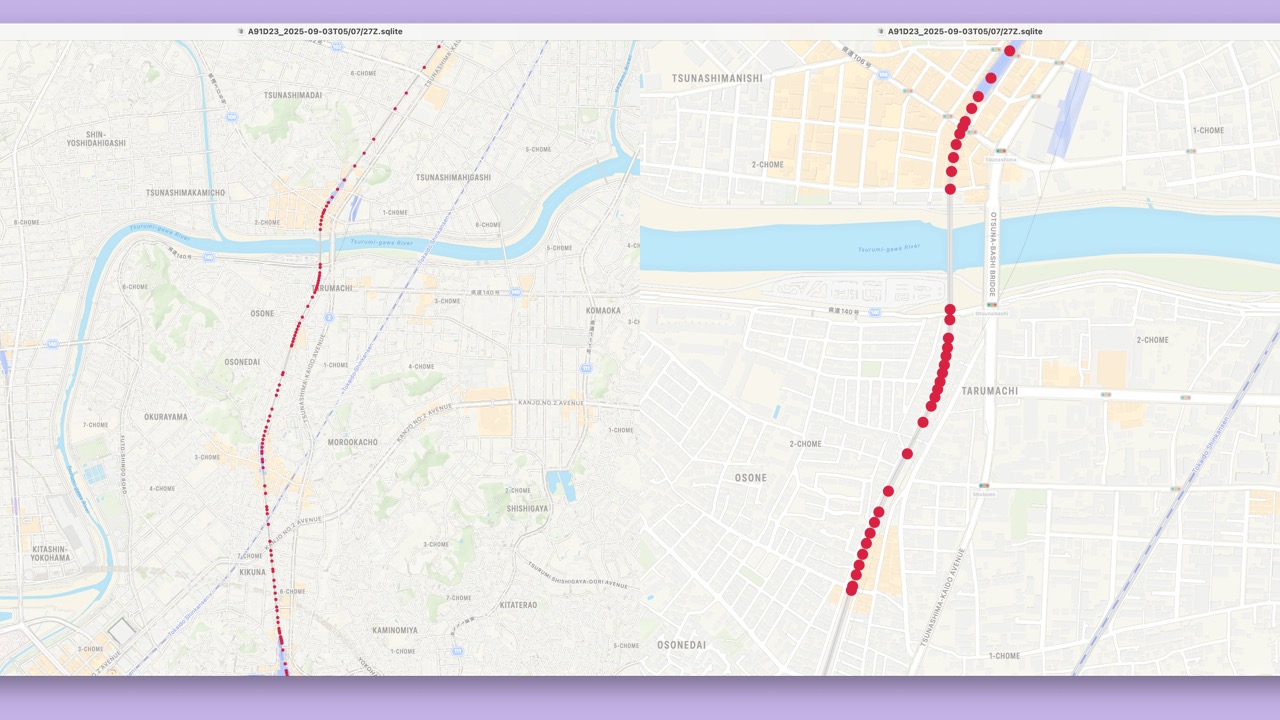
- We do have coordinates that outline the railway…

- First, we find the closest
RailwayCoordinateto theLocationfor each Railway. - Then, we order the Railways by which
RailwayCoordinateis nearest.
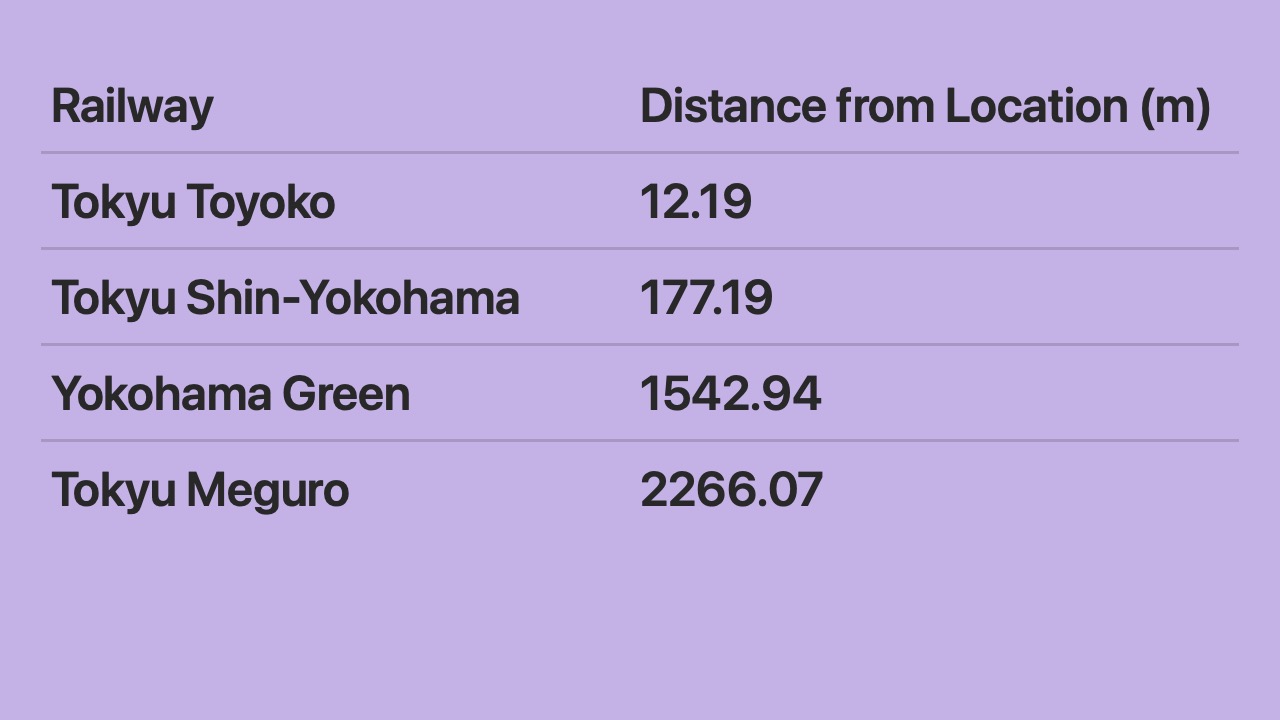
- Here are our results.
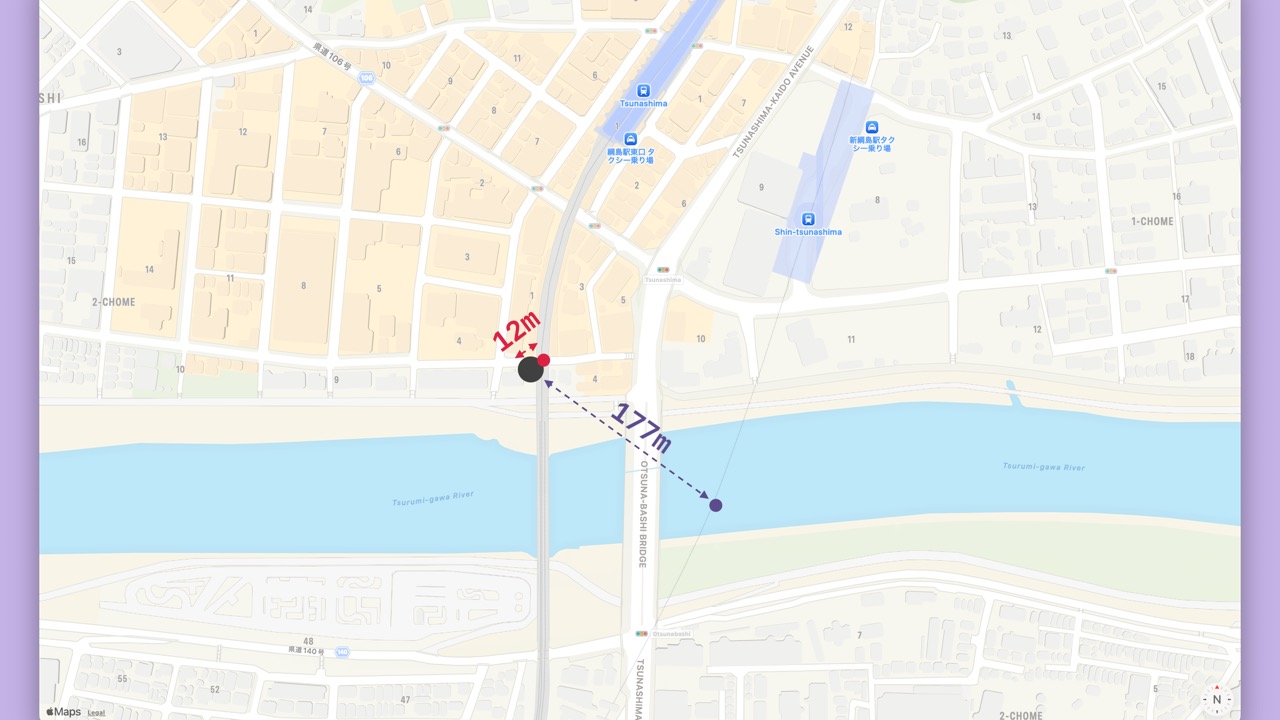
- The closest
RailwayCoordinateis from the Toyoko Line at only 12 meters away. - The next closest
RailwayCoordinateis from the Shin-Yokohama Line at 177 meters away.
- We did it!
- Our algorithm works well for this case.
- But…
- Let’s consider another
Location. - This
Locationwas also captured on the Toyoko Line.
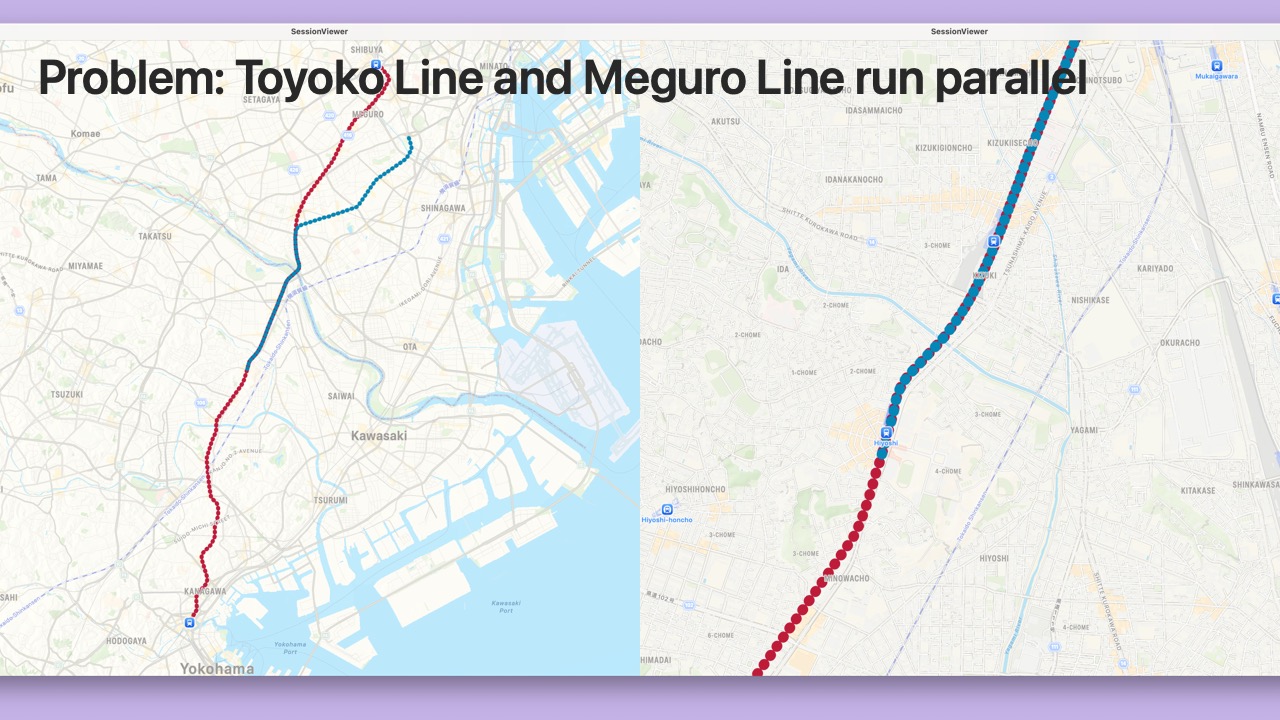
- But in this section of the railway track, the Toyoko Line and Meguro Line run parallel.
- It’s not possible to determine whether the correct line is Toyoko or Meguro from just this one
Location.
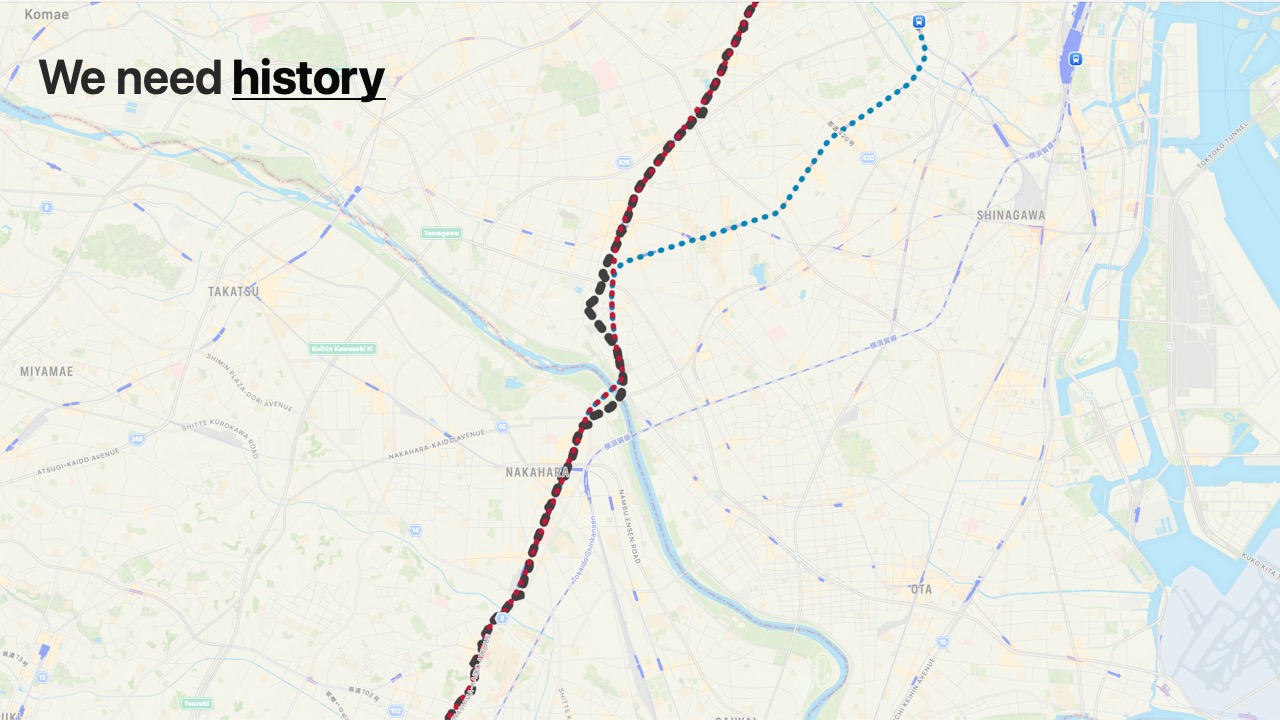
- The algorithm needs to use all
Locations from the journey. - The example journey follows the Toyoko Line for longer than the Meguro Line.

- First, we convert the distance between the
Locationand the nearestRailwayCoordinateto a score. - The score is high if close and exponentially lower when far.
- Then, we add the scores over time.

- The score from Nakameguro to Hiyoshi is now higher for the Toyoko Line than the Meguro Line.
- We did it!
- Our algorithm works well for this case.
- But…
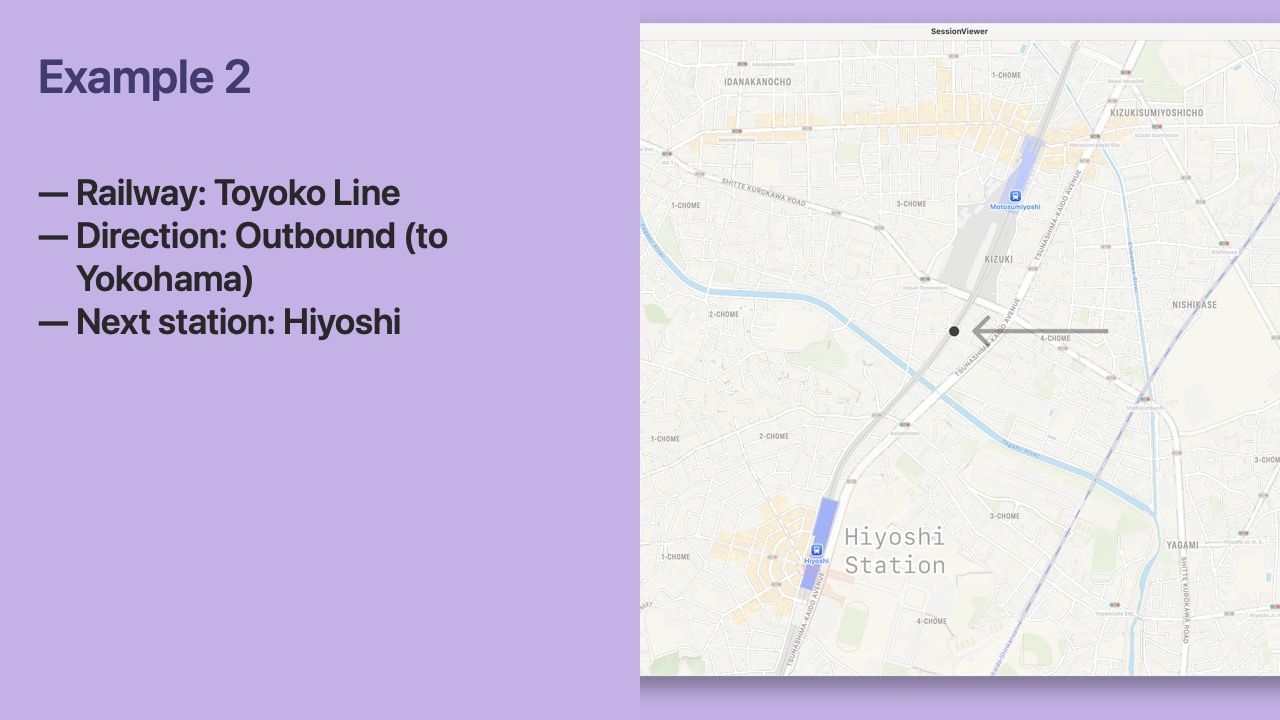
- Let’s consider a third
Location. - This
Locationwas captured on the Keihin-Tohoku Line which runs the east corridor of Tokyo.
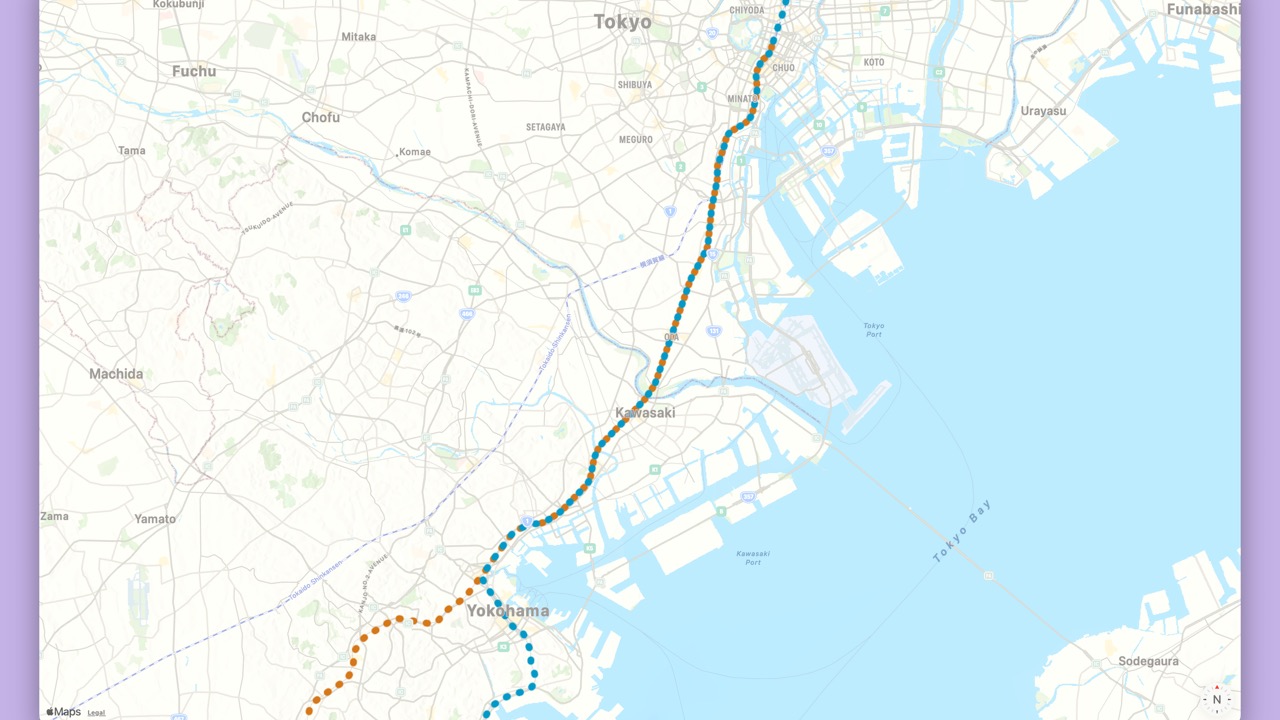
- Several lines run parallel in this corridor.
- The Tokaido Line follows the same track as the Keihin-Tohoku Line
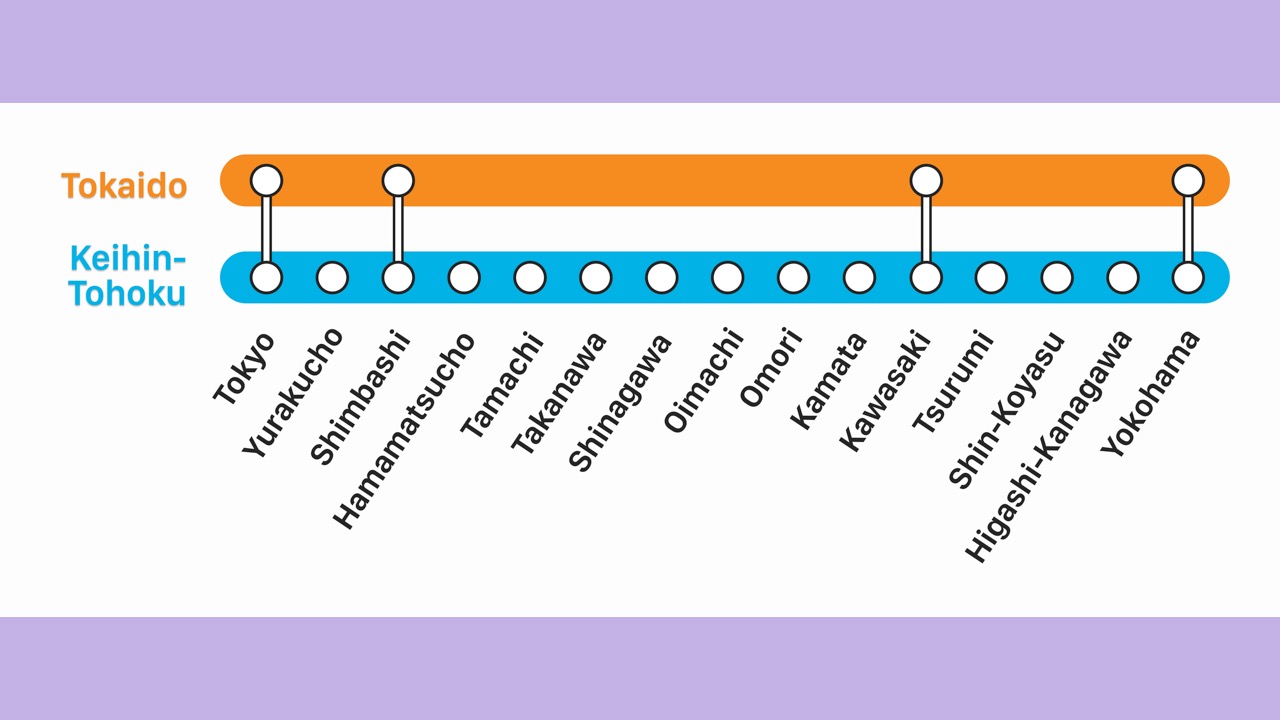
- But the Tokaido Line skips many stations.
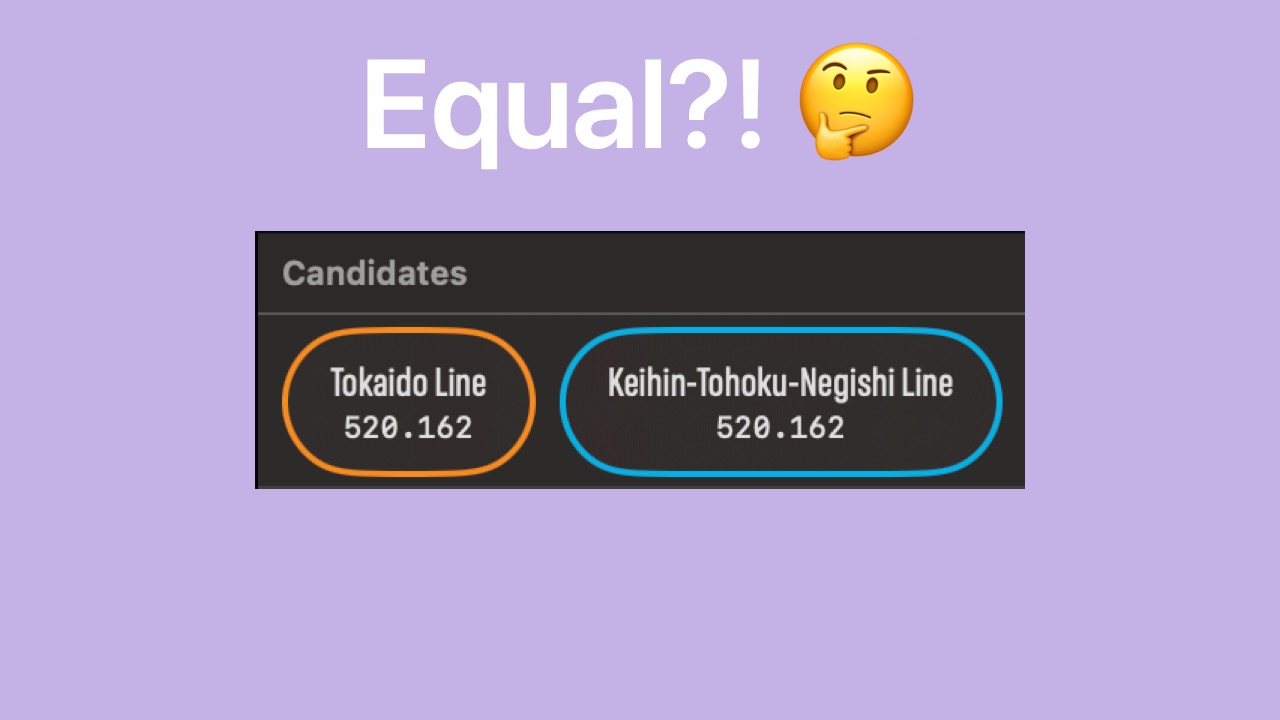
- If we only compare railway coordinate proximity scores, the scores will be the same.

- Let’s add a small penalty to the score if a station is passed.
- If a station is passed, that indicates the iPhone may be on a parallel express railway.
- Let’s also add a small penalty to the score if a train stops between stations.
- If a train stops between stations, that indicates the iPhone may be on a parallel local railway.

- Using this algorithm, the Keihin-Tohoku score is now slightly larger than the Tokaido score.

- Let’s consider two example trips to better understand penalties.
- For an example trip 1 that starts at Tokyo station…

- The train stops at the second Keihin-Tohoku station.
- The Tokaido score receives a penalty since the stop occurs between stations.

- As we continue…

- The Tokaido score receives many penalties.
- Therefore, the algorithm determines the trip was on the Keihin-Tohoku Line.

- For an example trip 2 that also starts at Tokyo…

- The train passes the 2nd Keihin-Tohoku station.
- And the Keihin-Tohoku score receives a penalty.

- As we continue…
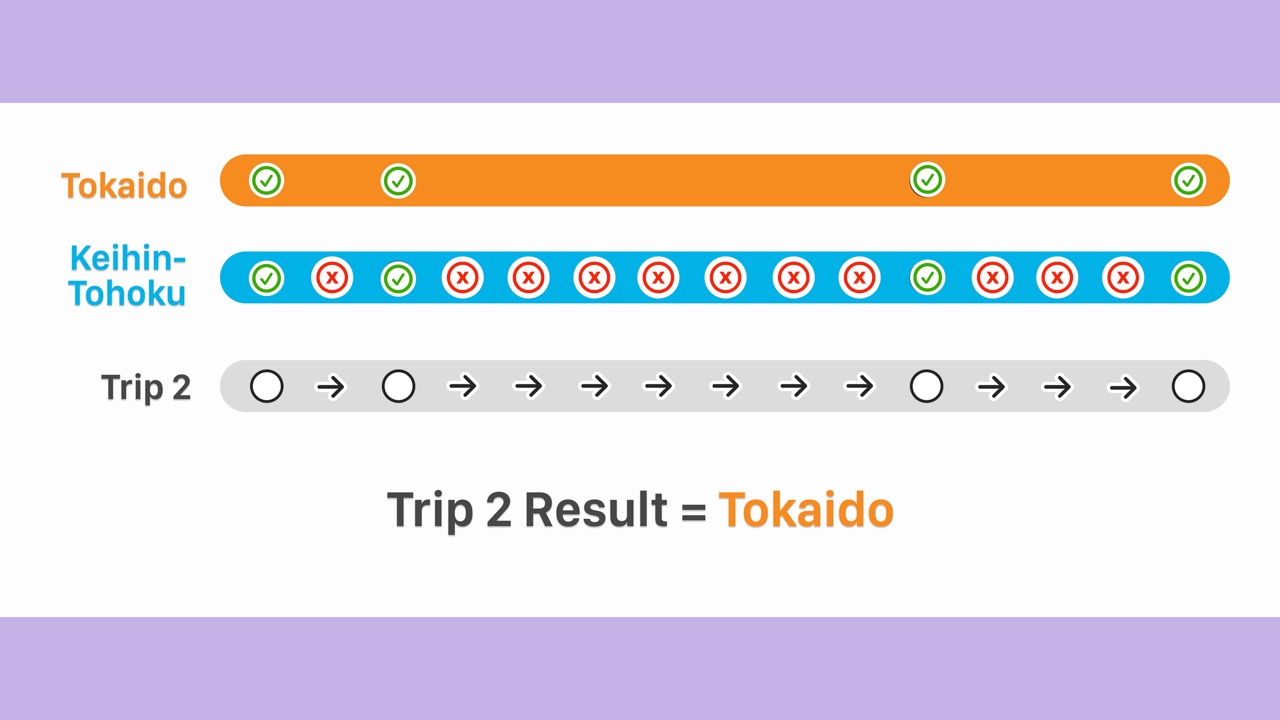
- The Keihin-Tohoku score receives many penalties.
- Therefore, the algorithm determines the trip was on the Tokaido Line.
- We did it!
- Our algorithm works well for this case.
- There are many more edge cases.
- However, let’s continue.

- For each potential railway, we will determine which direction the train is moving.

- Every railway has 2 directions.
- We’re used to seeing separate timetables on the departure board at a non-terminal station.
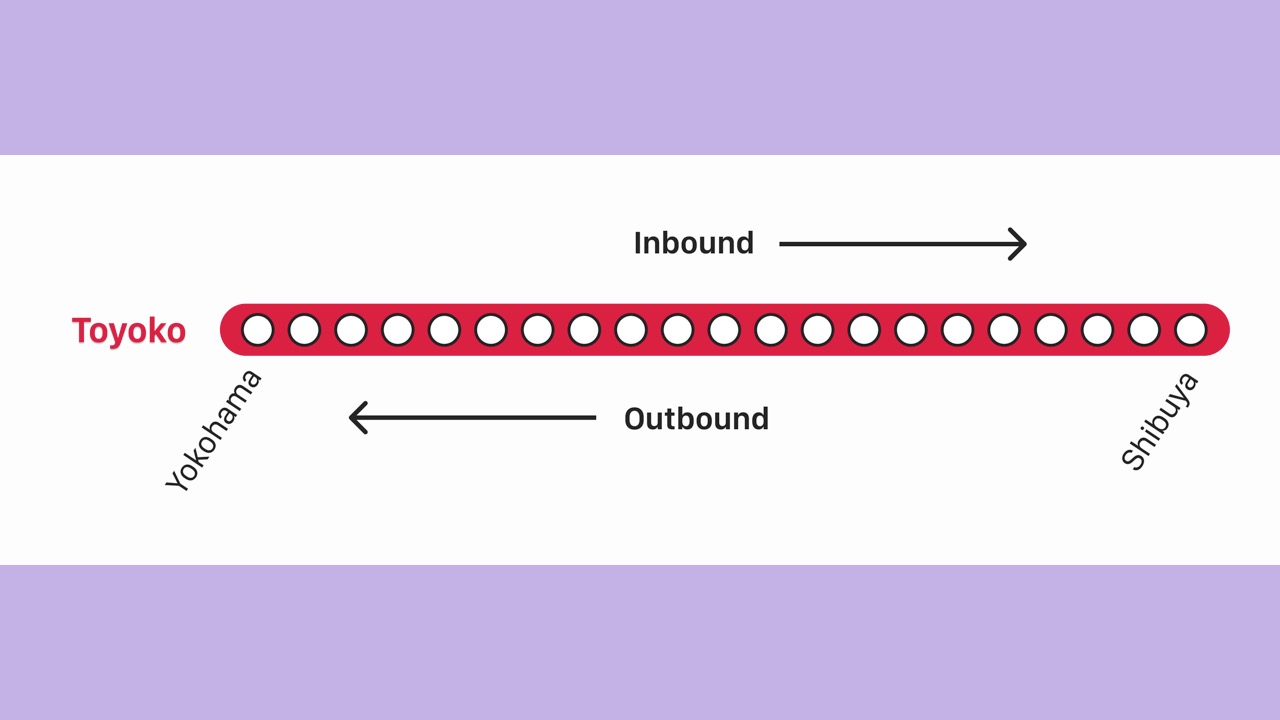
- For example, the Toyoko Line goes inbound towards Shibuya and outbound towards Yokohama.
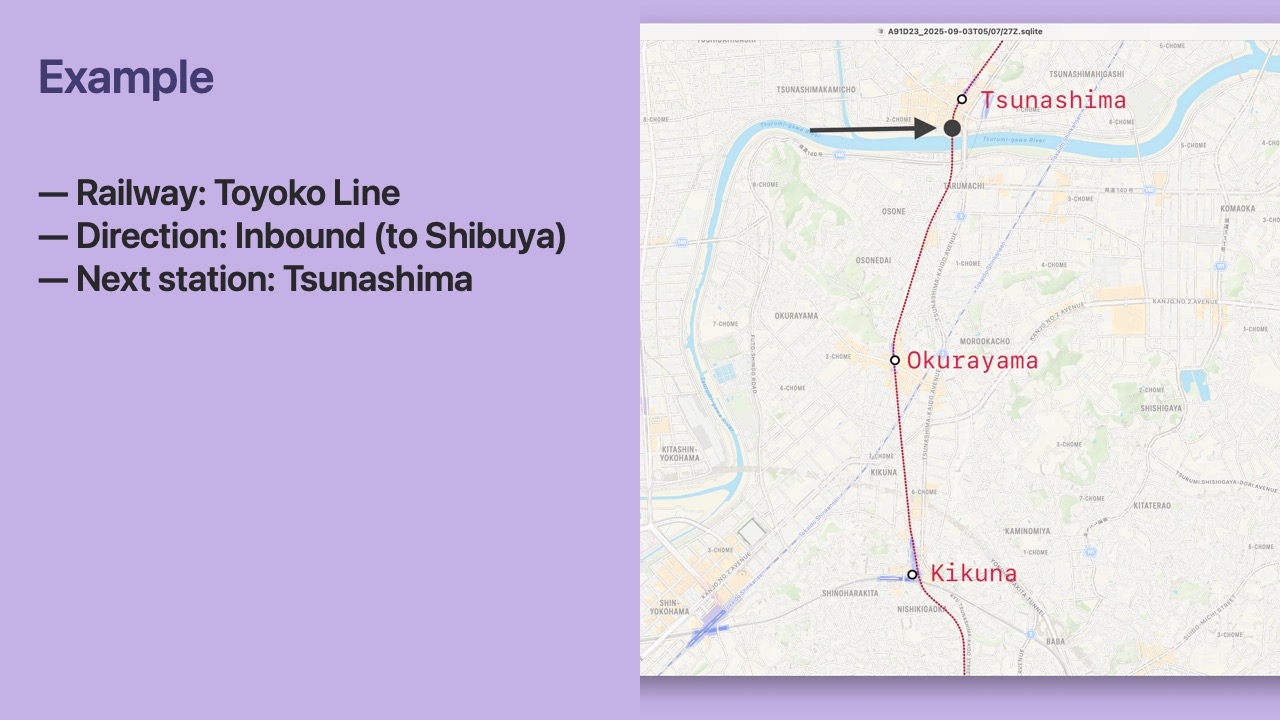
- Let’s consider a
Locationcaptured on the Toyoko Line going inbound to Shibuya.

- Once we have visited two stations, we can compare the temporal order the station visits.
- If the visit order matches the order of the stations in the database, we say that the iPhone is heading in the “ascending” direction.
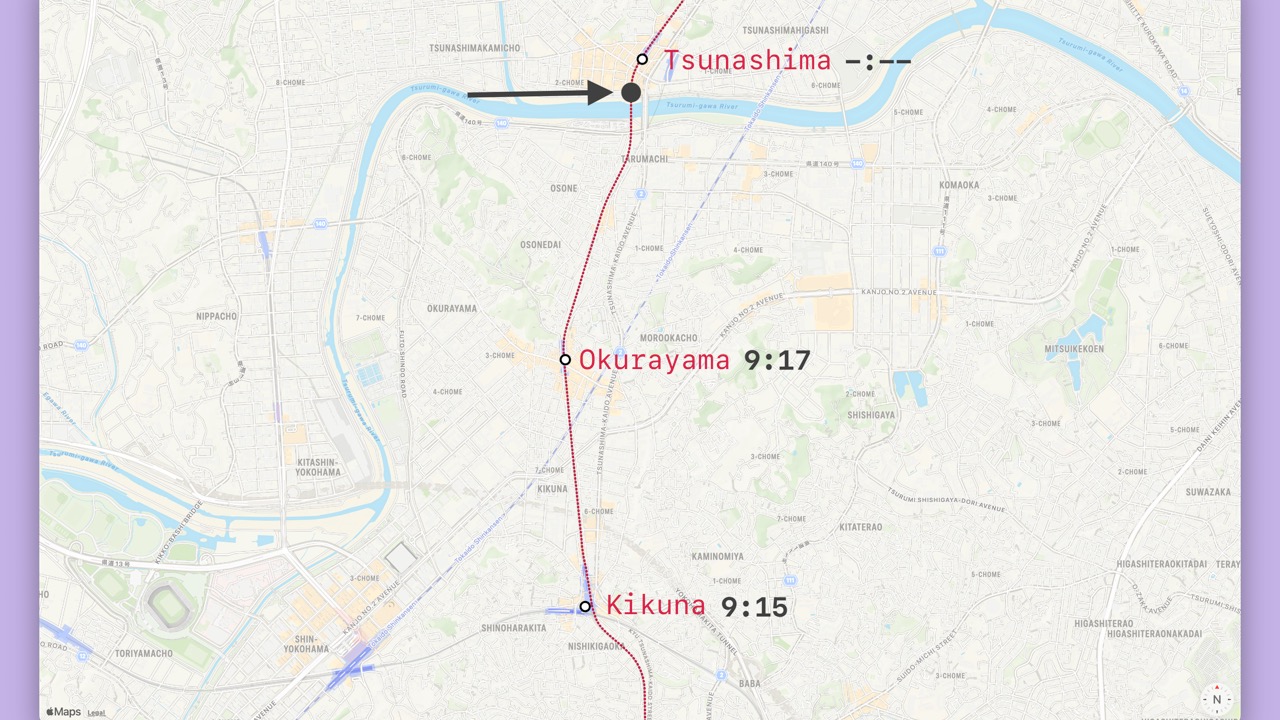
- The iPhone visited Kikuna and then Okurayama.
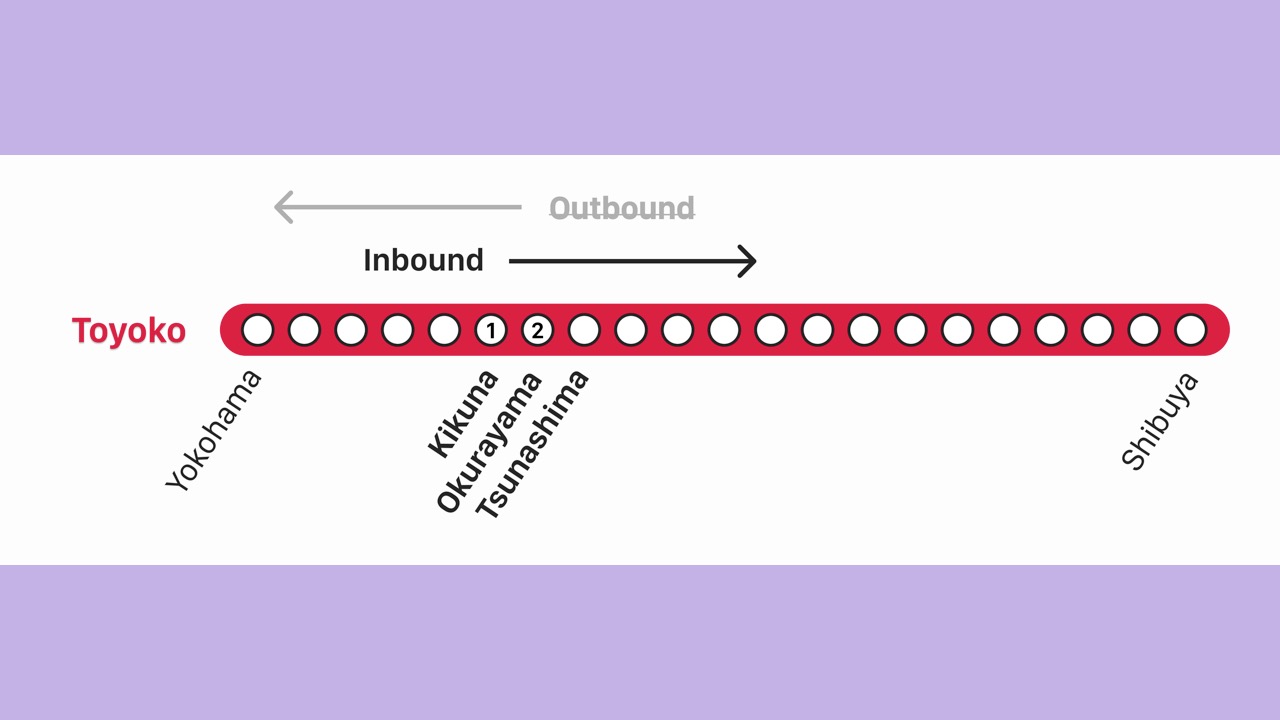
- This ordering does not match the database, so we consider it “descending”.
- In the database, “descending” maps to inbound.
- Therefore, we know the iPhone is heading inbound to Shibuya.
- We did it!
- Our algorithm works well for this case.
- But…
- It could take 5 minutes to determine the train direction.
- Can we do better?
- Let’s use the
Location’s course. - Remember that course is included with some
CLLocations by Core Location. - Several points moving at a decent speed are required before Core Location adds course to a
CLLocation. - And course itself has its own accuracy value included.
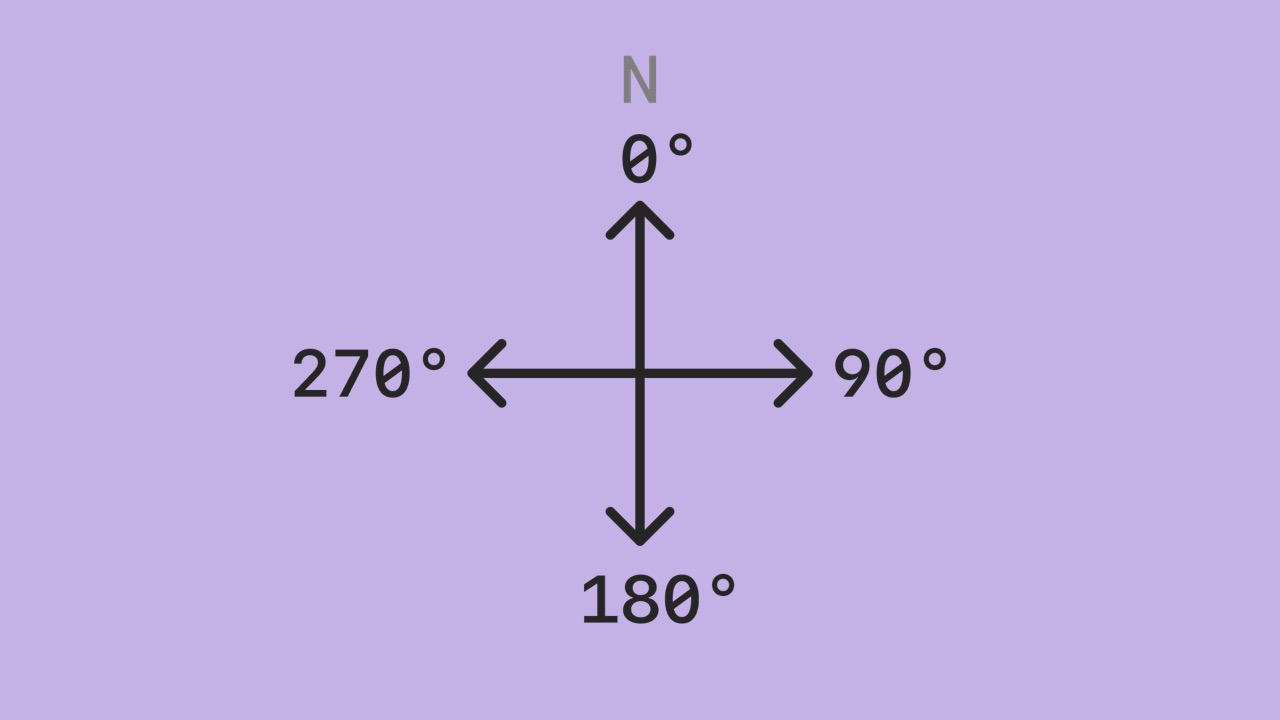
- Core Location provides an estimate of the iPhone’s course in degrees.

- Note that this is not the iPhone’s orientation using the compass.
- The course value should be the same regardless of whether the iPhone is in a pocket or held in a hand facing the rear of the train.
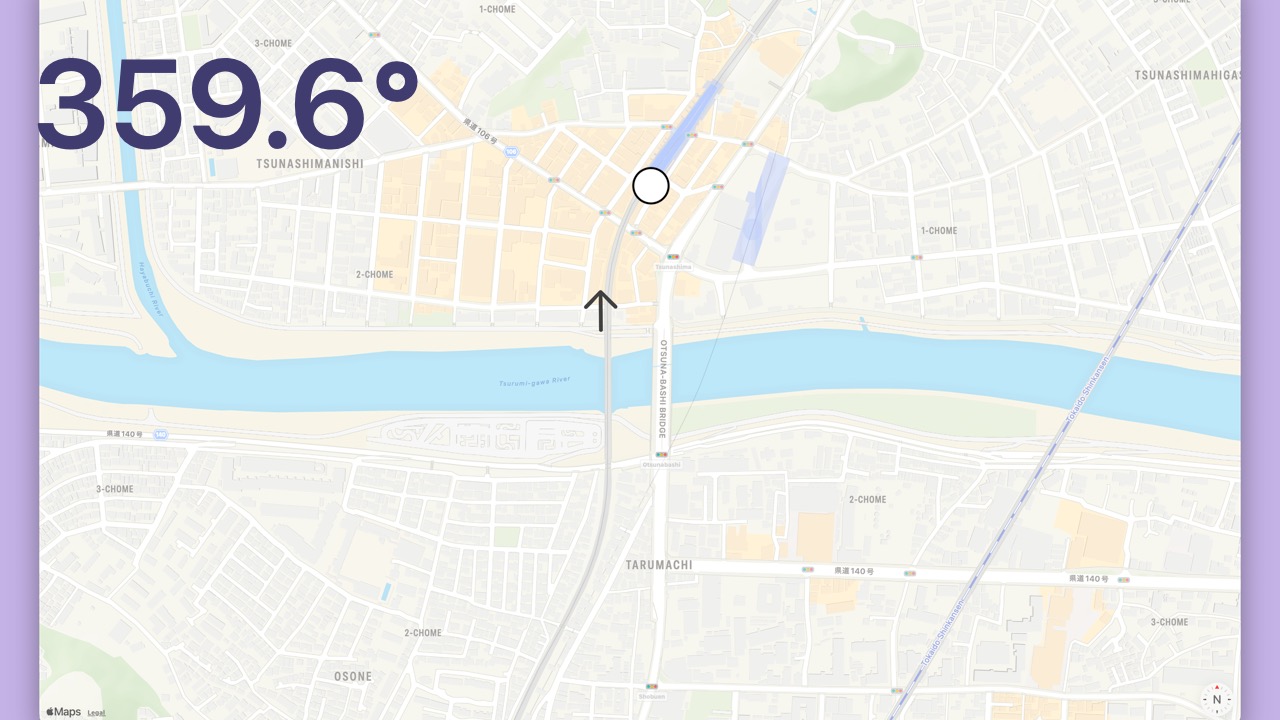
- The course for the example
Locationis 359.6 degrees. - It’s almost directly North.
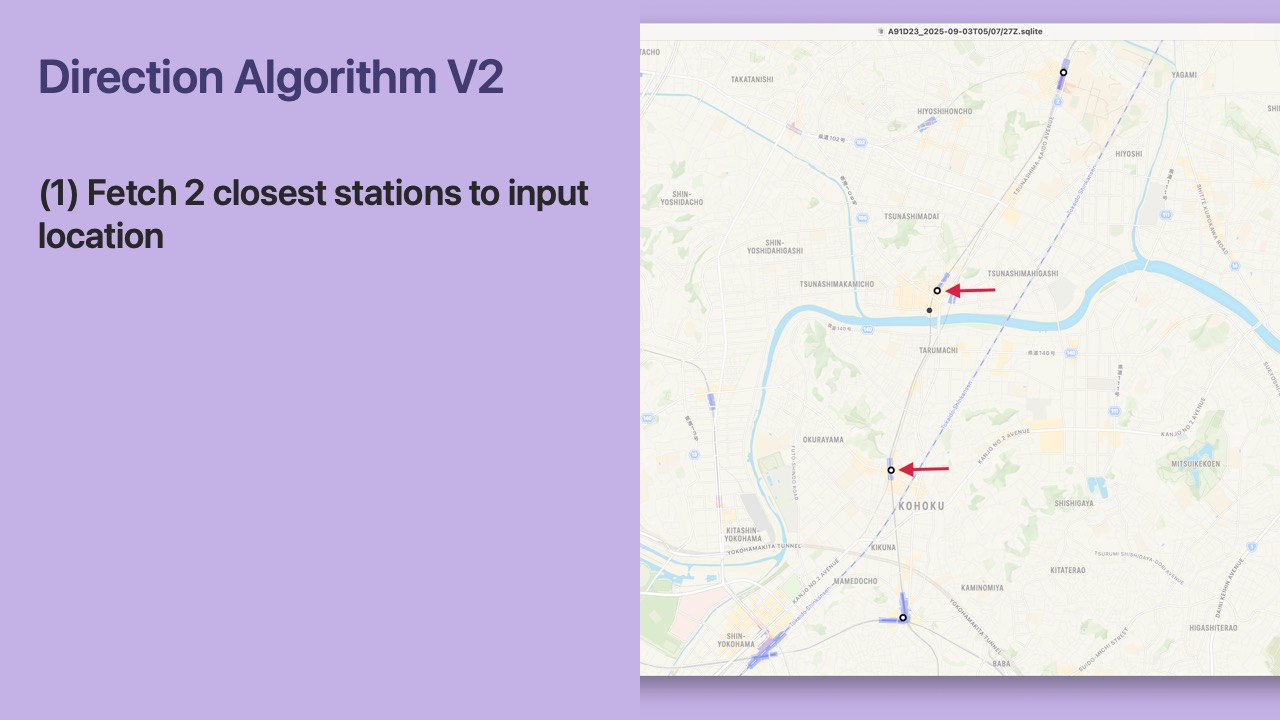
- First, we find the 2 closest stations to the
Location
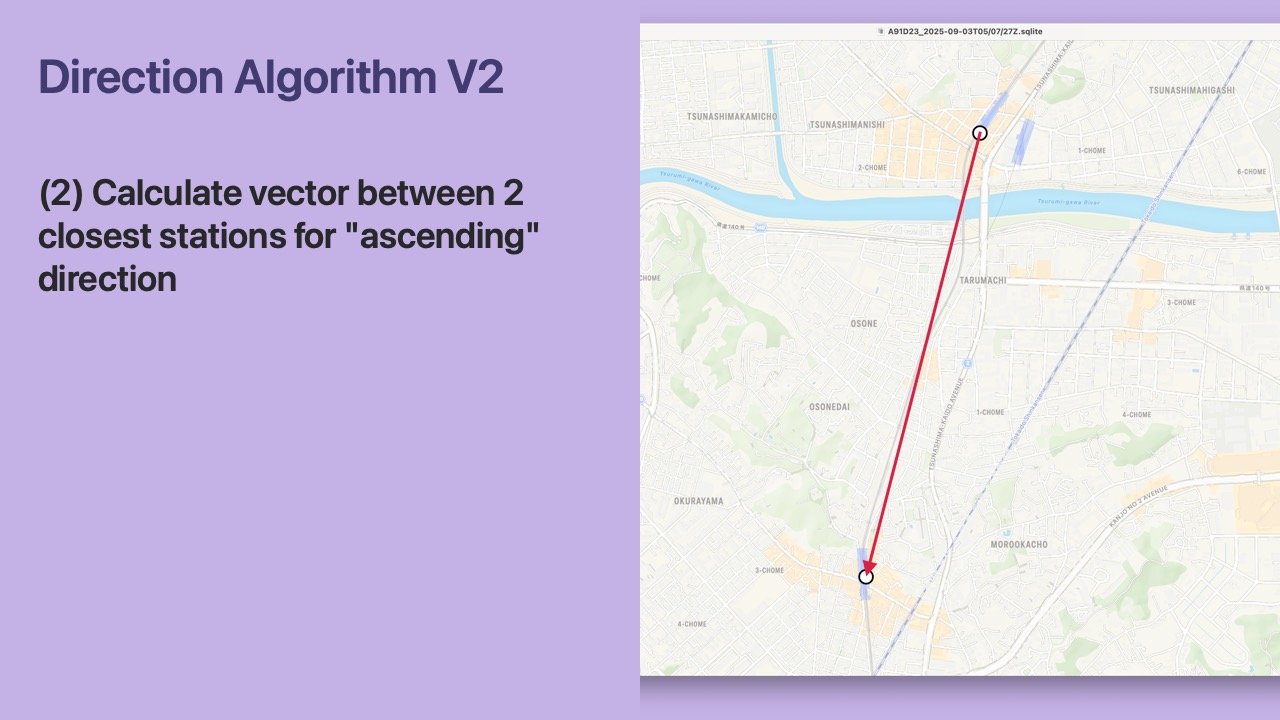
- Next, we calculate the vector between the 2 closest stations for the “ascending” direction in our database.
- For the Toyoko line, the “ascending” direction is outbound (as mentioned earlier).
- Therefore the vector goes from Tsunashima to Okurayama.

- We need to take a quick sidebar to talk about the dot product.
- Do you remember the dot product from math class?
- We can compare the direction of unit vectors with the dot product.
- Two vectors facing the same direction have a positive dot product.
- Two vectors facing in opposite directions have a negative dot product.

- Next, we calculate the dot product between the
Location’s course vector and the stations vector. - If the dot product is positive, then the railway direction is “ascending”.
- If the dot product is negative, then the railway direction is “descending”.

- The dot product is -0.95.
- It’s negative.
- Negative means “descending”.
- And “descending” in our database maps to inbound for the Toyoko Line.
- Therefore, the iPhone is heading to Shibuya.
- We did it!
- Our algorithm works well.
- Let’s move on to the last part of the algorithm.

- Finally, we can determine the next station.

- The next station is shown on the train information display.
- We’ll call this the “focus station phase” going forward.
- This includes the station name (e.g. Kikuna) and its phase (e.g. Next).

- The display cycles through next, soon, and now phases for each station.
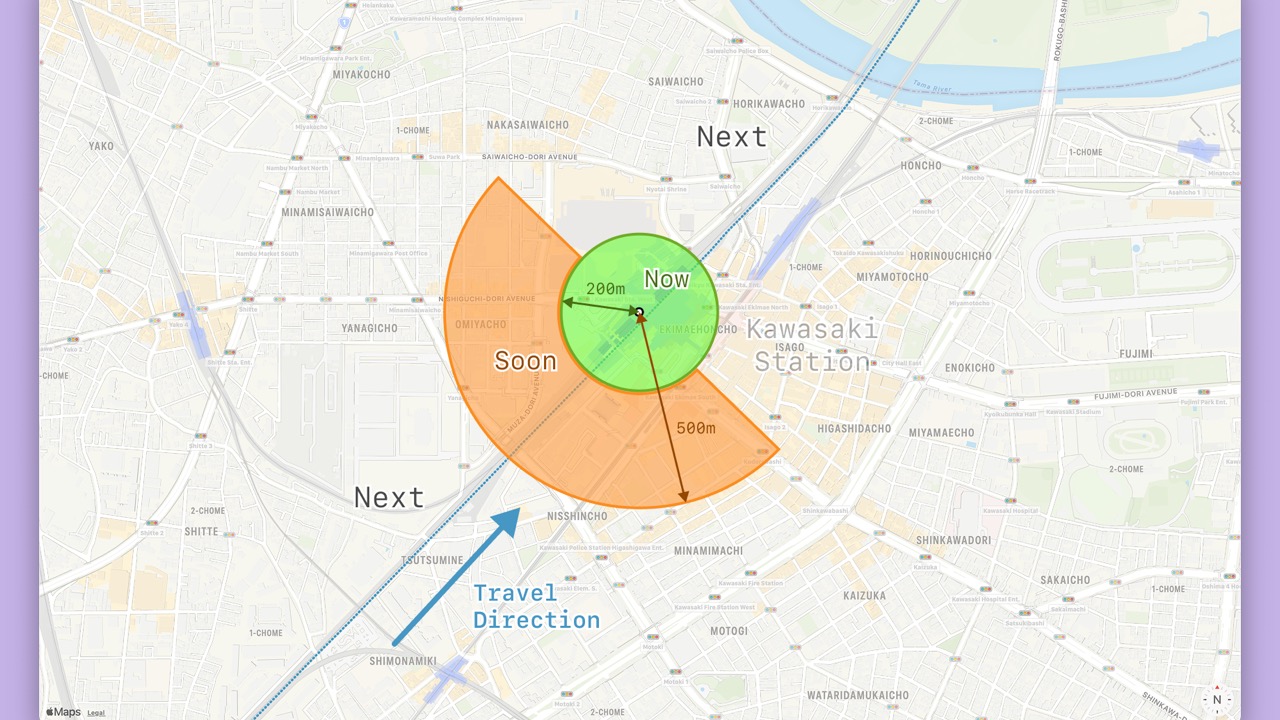
- On a map, here is where we will show each phase.

- We calculate the distance
dand direction vectorcfrom theLocationto the closest station. - We show the closest station
Sor the next station in the travel directionS+1depending ondandc.
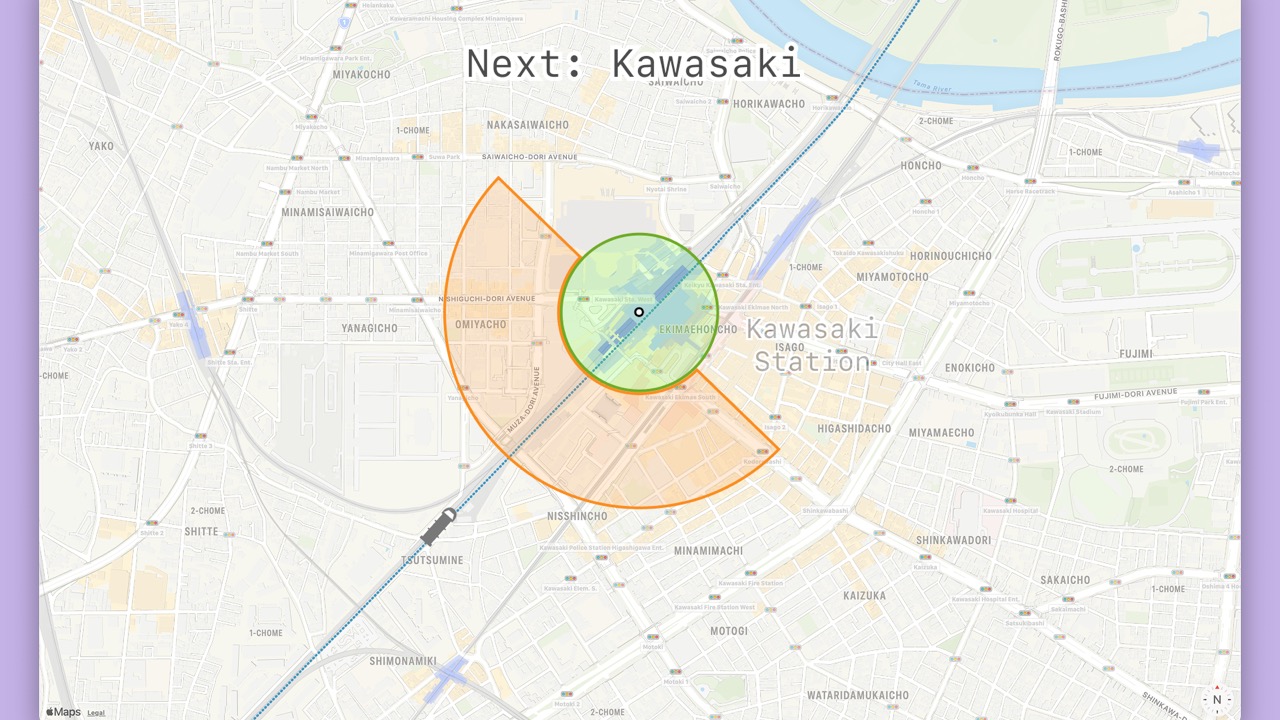
- When the closest station is in the travel direction, the phase will be “next”.
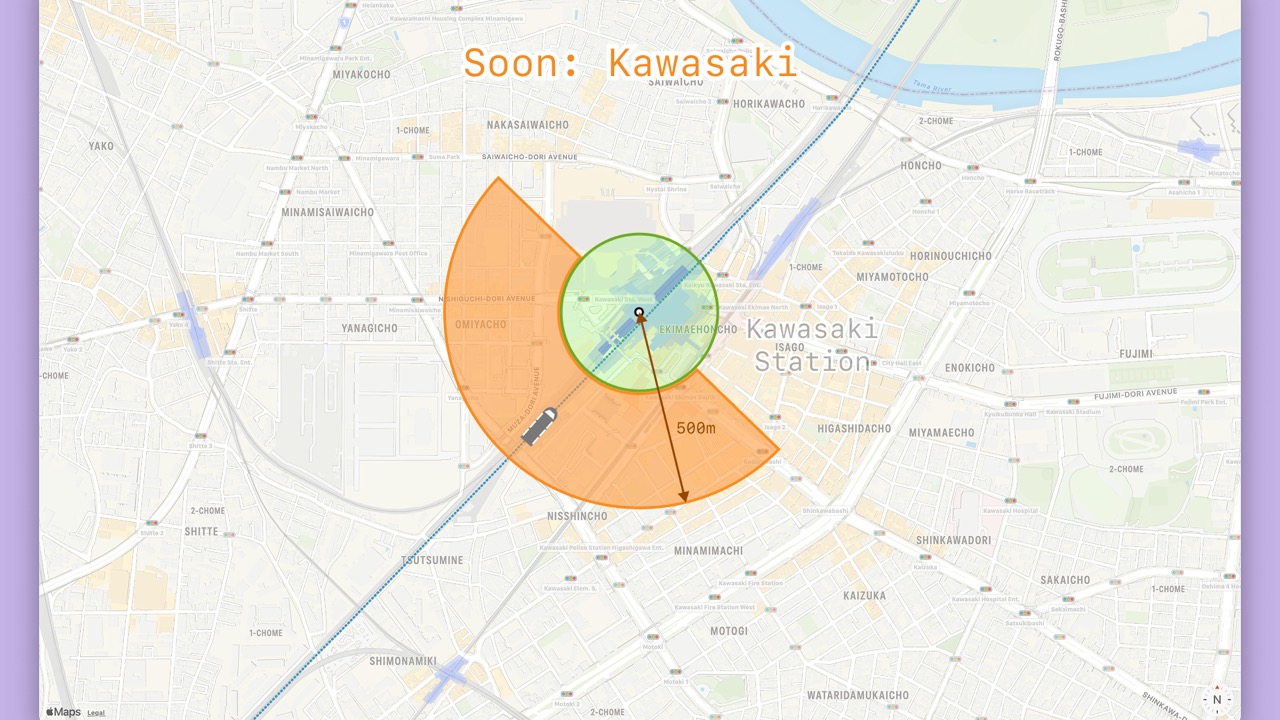
- A
Locationless than 500m from the station will be “soon”.
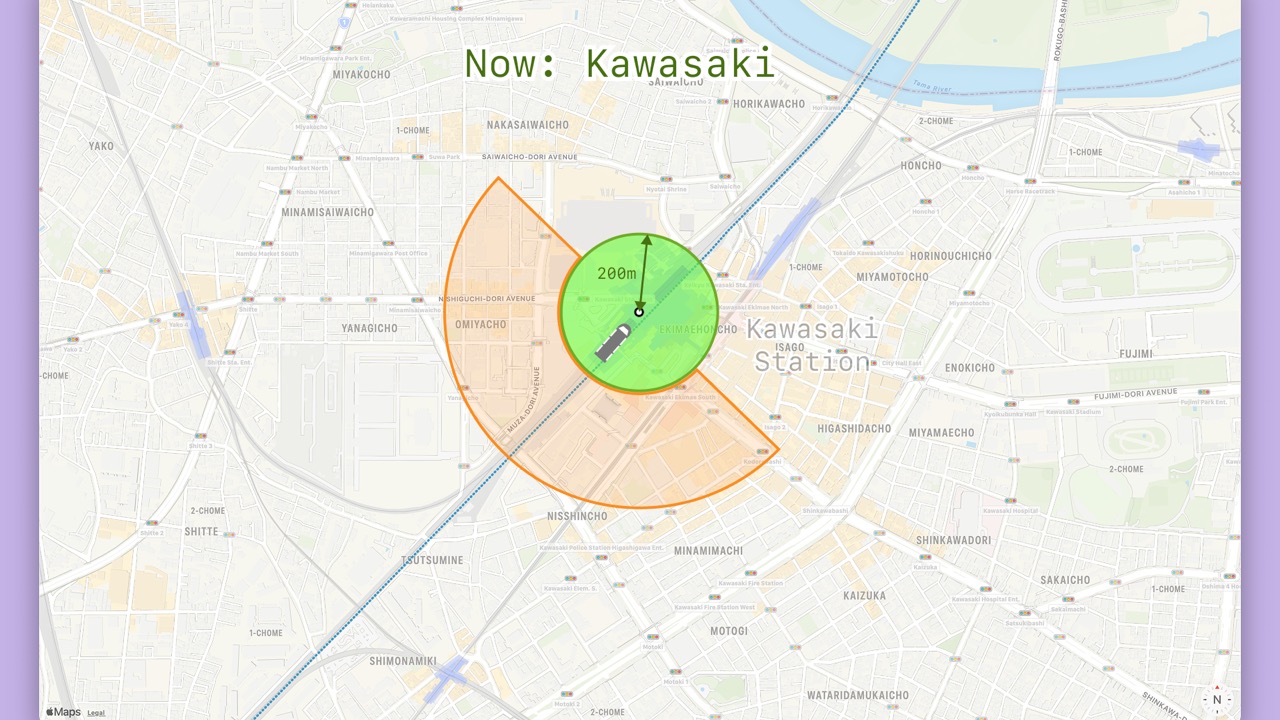
- A
Locationless than 200m from the station will be “now”.
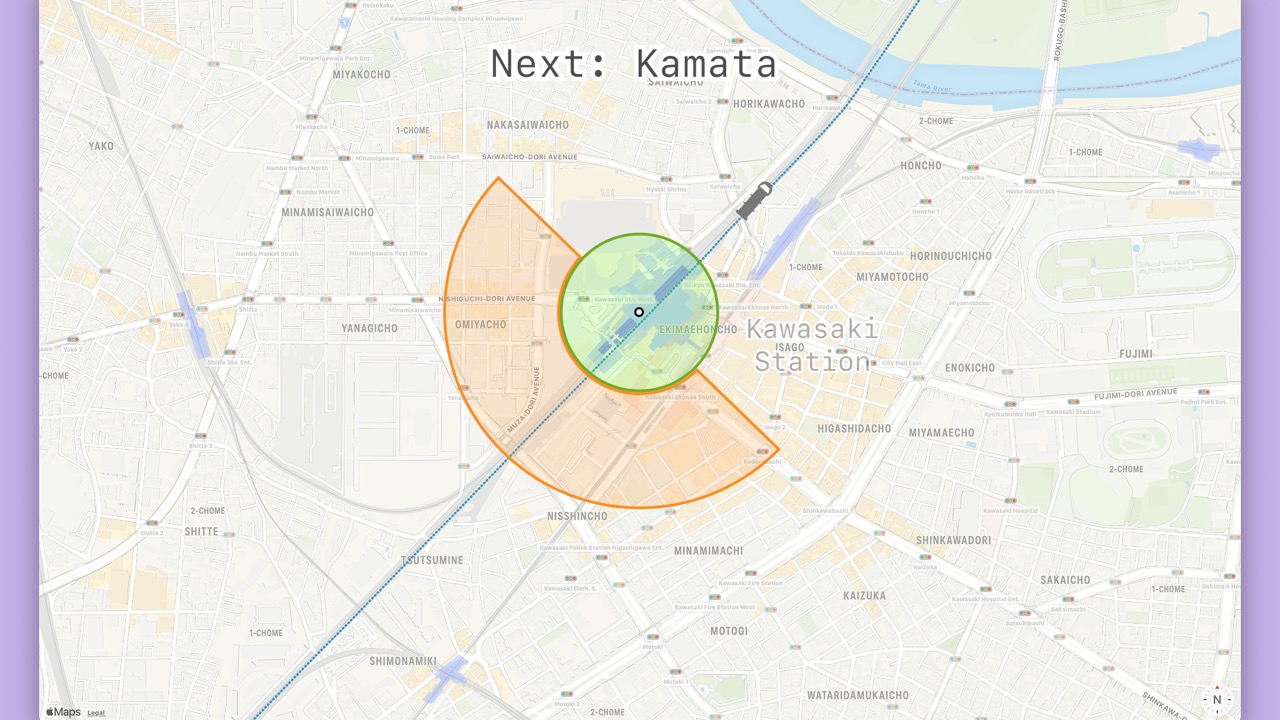
- Even though the
Locationis within 500m from the closest station, the station is not in the travel direction. - Therefore, the phase will be “next” for the next station in the travel direction.
- We did it!
- Our algorithm works well.
- But…

- GPS data is unreliable.
- Especially within big stations.
- Especially when not moving.
- Here is an example
Locationstopped inside Kawasaki station that has an abysmal 1 km accuracy.

- Let’s create a history of
Locations for each station. - For each station, let’s categorize each
Locationaccording to its distance and direction.
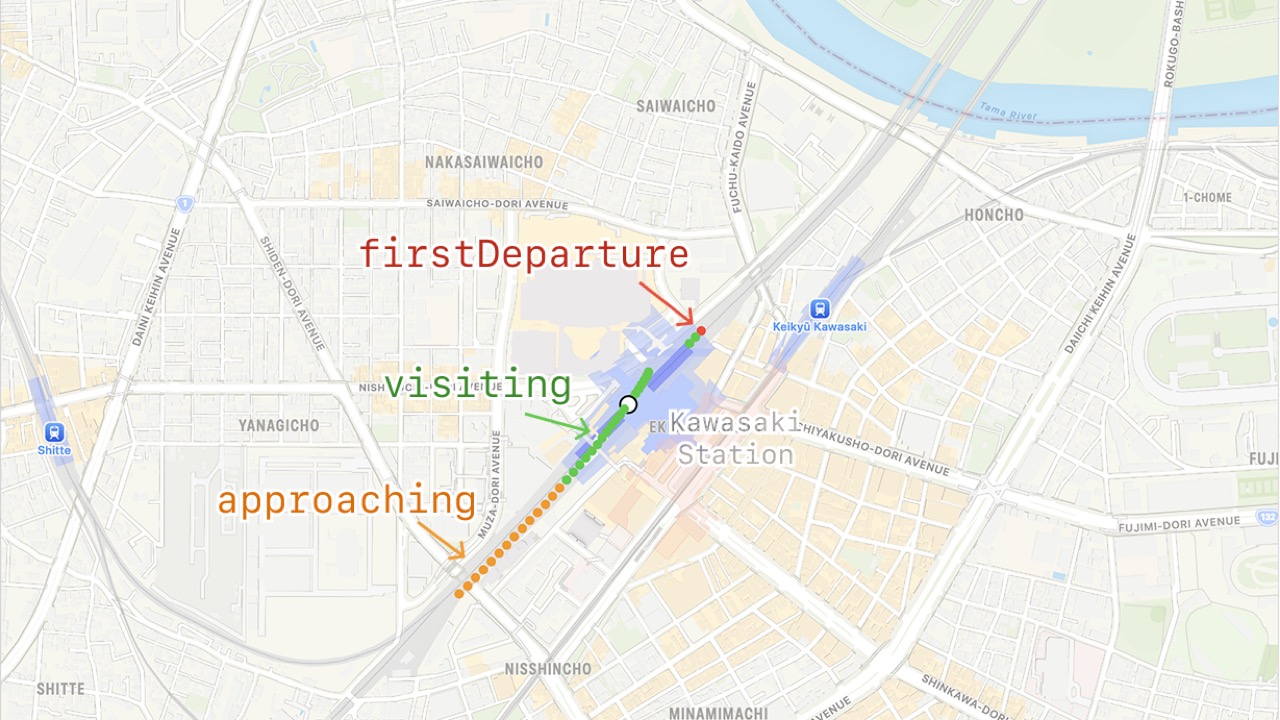
- In this example, “approaching” points are orange, “visiting” points are green, and the departure point is “red”.

- Focus station algorithm version 2 has 3 steps.
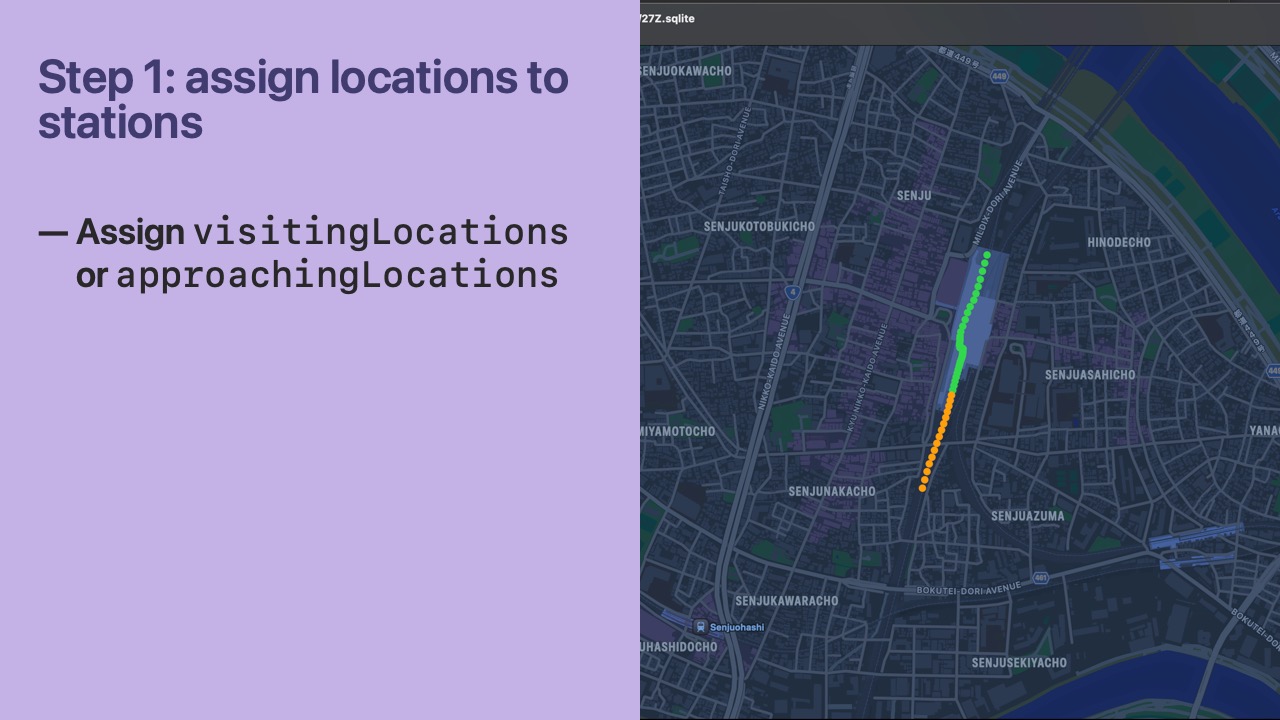
- In step 1, we categorize a
Locationas “visiting” or “approaching” if it lies within the bounds of a Station. - Our rule is that only 1 Station per Railway will store a unique
Locationin thevisitingLocationsorapproachingLocationsarray. - Usually, this is not an issue, but some Stations on the same Railway are within 200m of each other.
- To disambiguate, we always choose the closest Station.
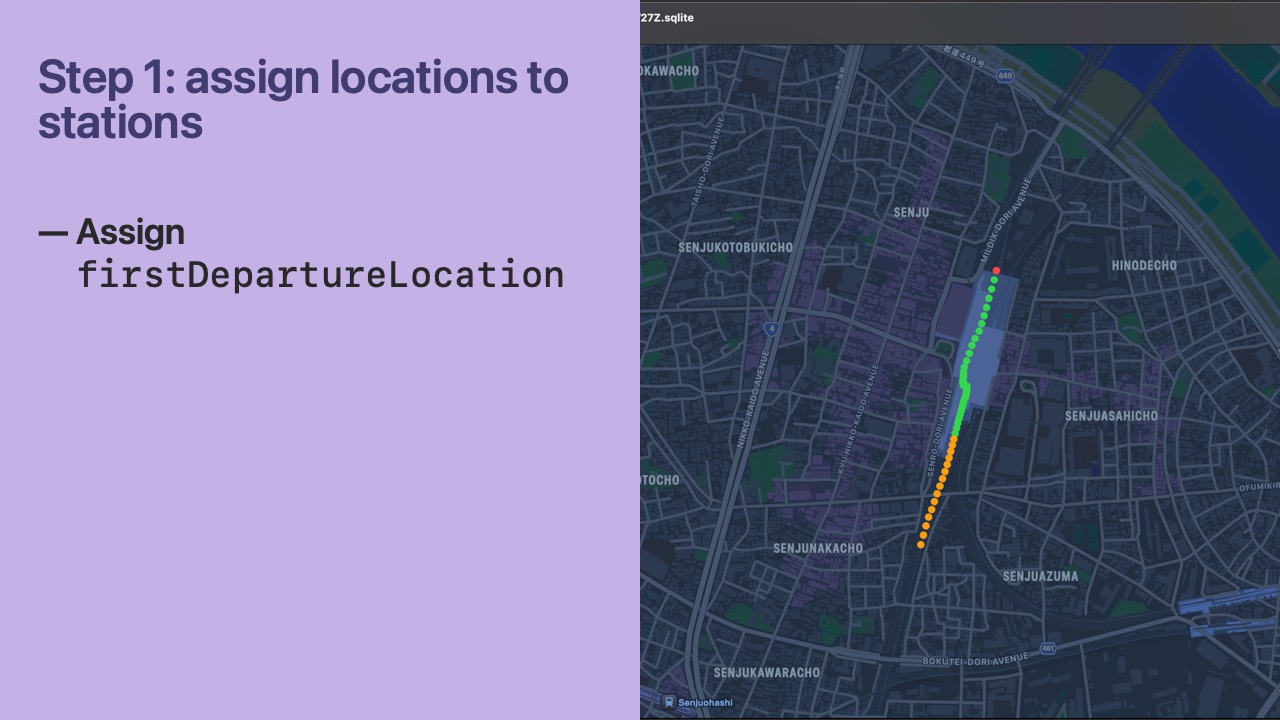
- If the
Locationis outside the bounds of any Station that already hasvisitingLocationsorapproachingLocationsas non-empty, we set thefirstDepartureLocationfor that Station. - It’s okay for a
Locationto be set asfirstDepartureLocationfor Station A while also being in avisitingLocationsorapproachingLocationsarray of Station B. - Additionally, there is special handling for the startup case where a railway has no
Locations set yet. In this case, we try to find the closestStationopposite the travel direction and set itsfirstDepartureLocation. - We can then consider that
Stationthe user’s departure station and use it to determine the focus station.

- In step 2, we use the station history to calculate the phase for each station.

- This is a departure phase for Minami-Senju station.
- The
StationDirectionalLocationHistoryhas only afirstDepartureLocation.
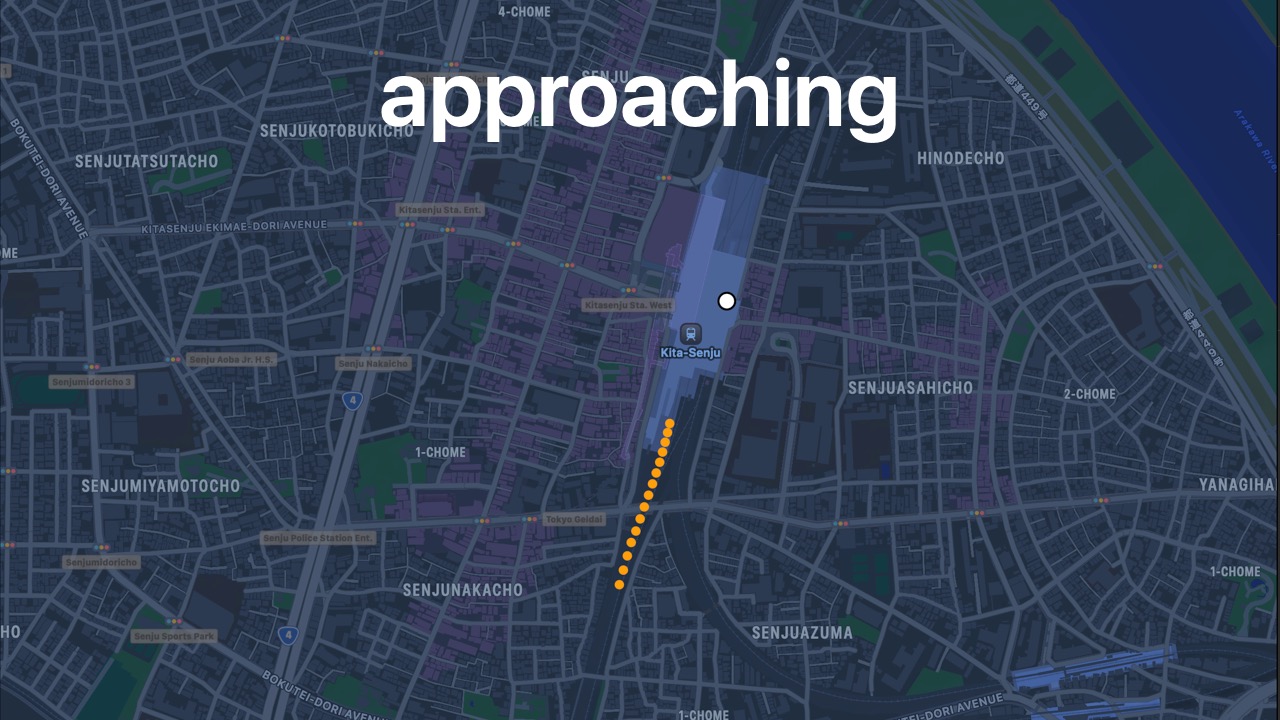
- This is an approaching phase for Kita-Senju station.
- Note: this would still count as an approaching phase even if there were only 1
Locationin theapproachingLocationsarray.
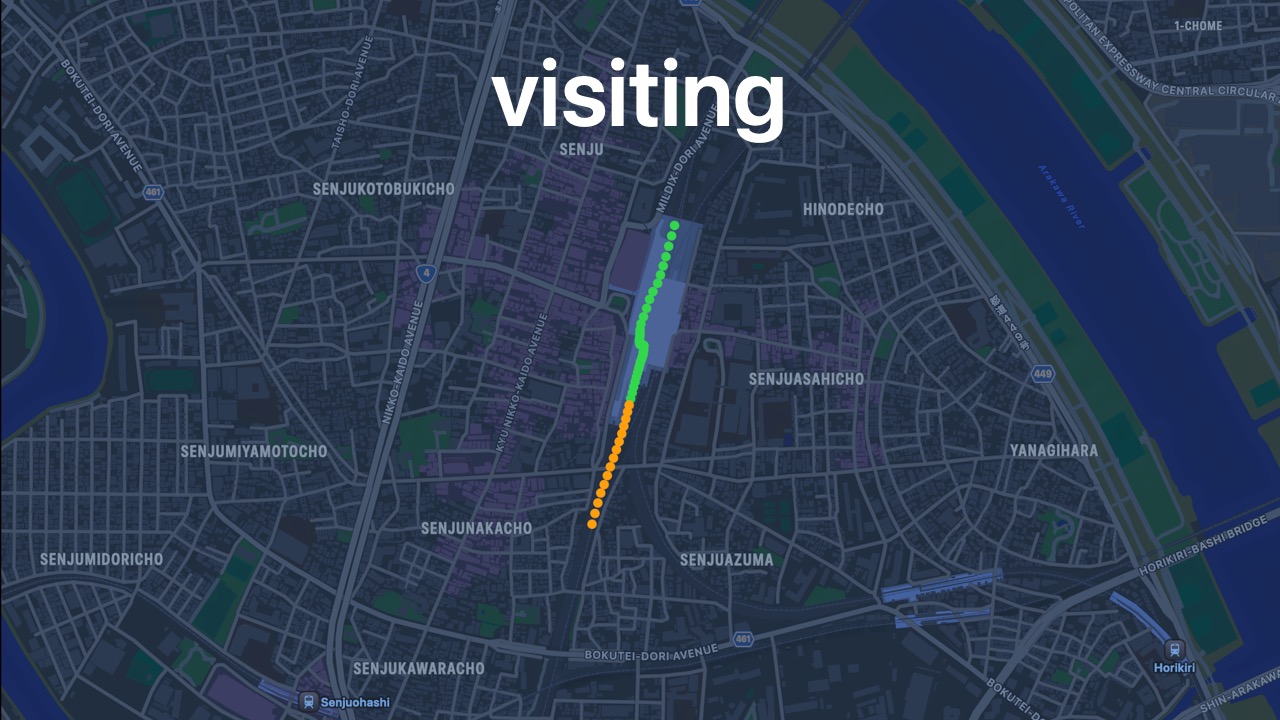
- This is a visiting phase.
- Note: this would still count as a visiting phase even if there were only 1
Locationin thevisitingLocationsarray.
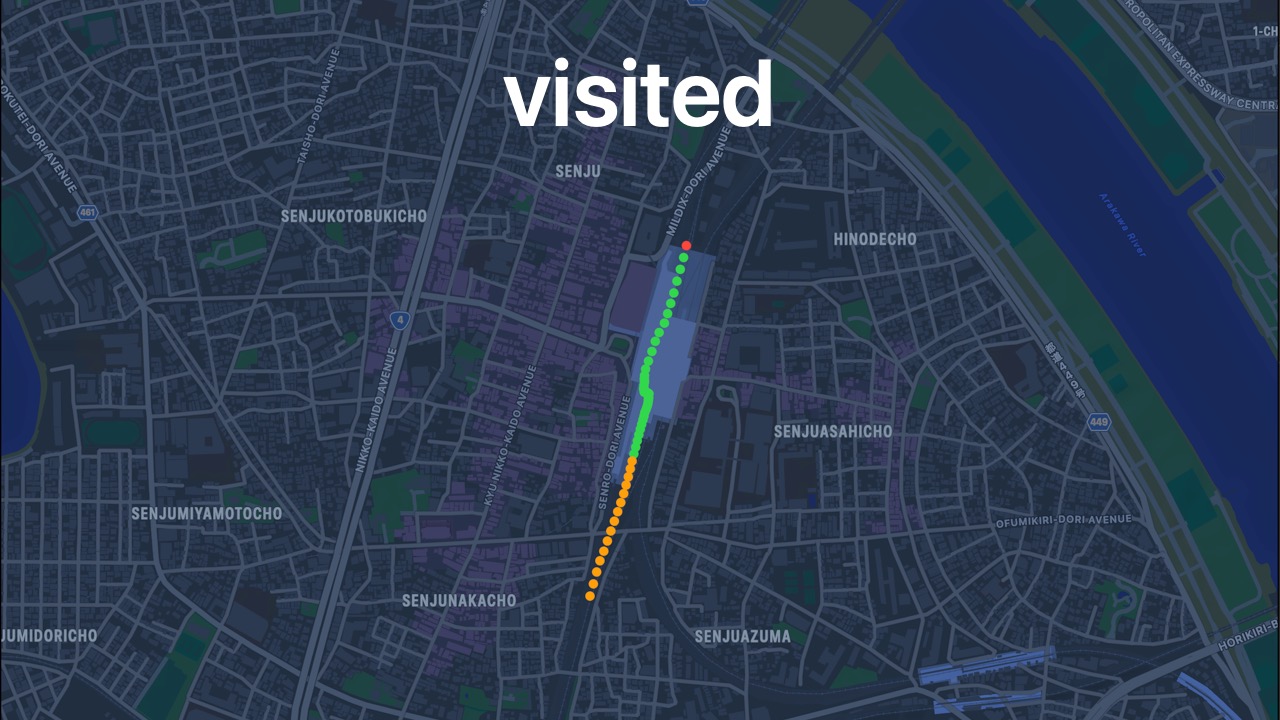
- This is a visited phase.
- You can see the
firstDepartureLocationin red.

- In step 3, we look through the station phase history for all stations to determine the focus station phase.
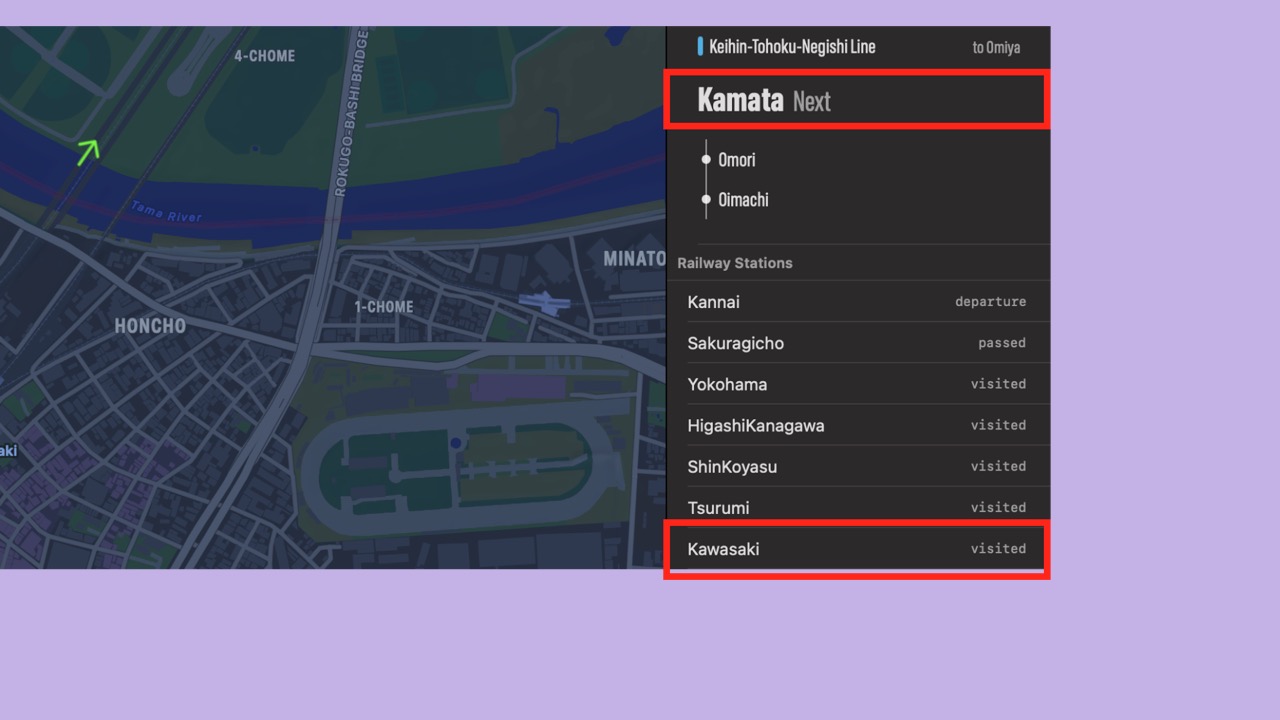
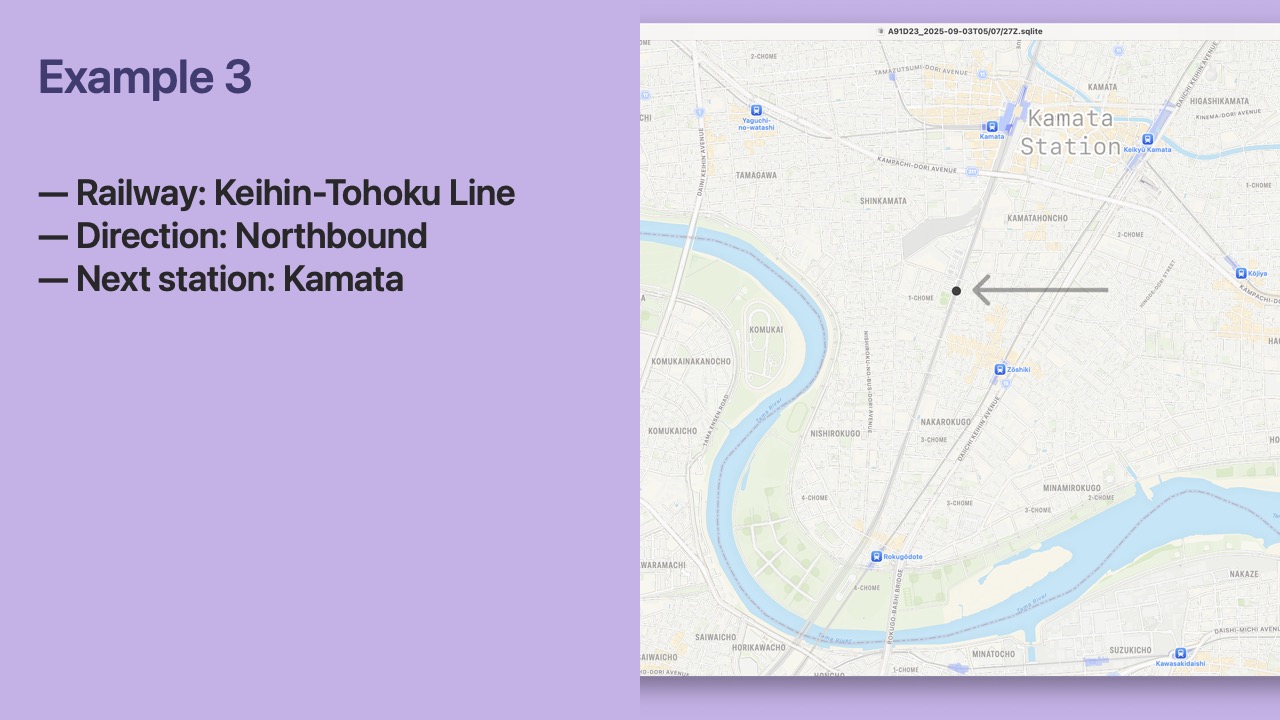
- In an example, when the latest phase for Kawasaki station is visited, then the focus phase is “Next: Kamata”
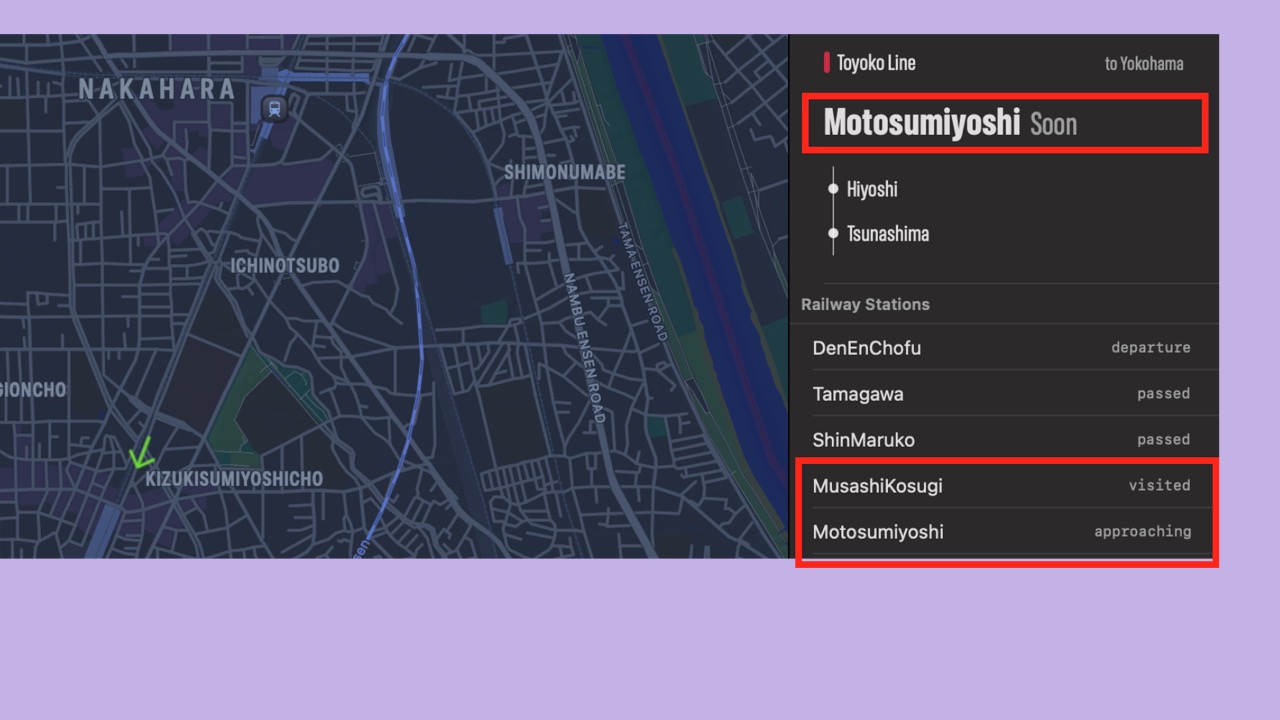
- In another example, when the latest station phase for Musashi-Kosugi station is visited and Motosumiyoshi station is approaching, then the focus phase is “Soon: Motosumiyoshi”
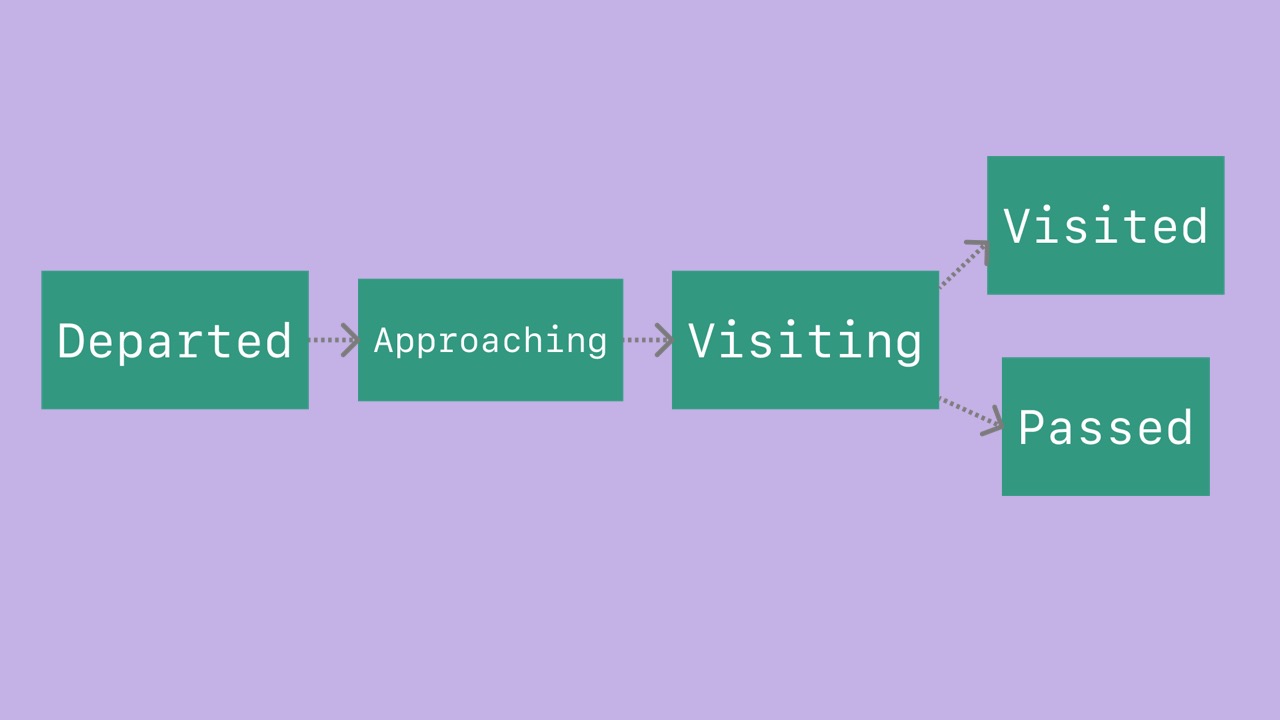
- Using a state machine gives us more stable results.
- We did it!
- Our algorithm works well…

- But can we tell the difference between a visited station and a passed station?
- Remember, we need this information to calculate a potential penalty for the railway score.
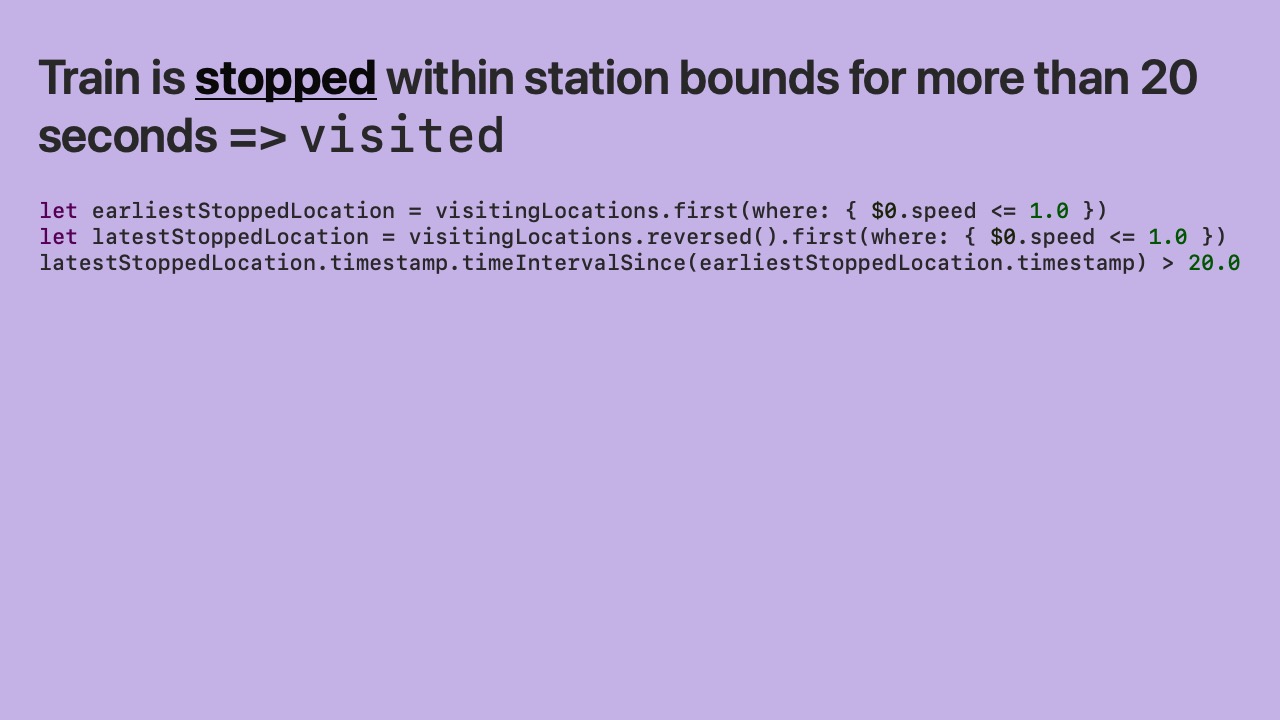
- If the train is stopped within a station’s bounds for more than 20 seconds then we consider it visited.

- If the train is moving within a station’s bounds for more than 70 seconds then we also consider it visited.
- This case is for stations with bad GPS reception.

- Otherwise we consider the station as passed.
- Now I’d like to demo the SessionViewer macOS app I created.
- I’ll show a journey from Kannai station to Kawasaki station on the Keihin-Tohoku line.
- It takes some time for all
Locations to be processed by the algorithm (top right). - But while it’s processing, I can start playback to see the journey at 10x speed (top right).
- In the inspector (right sidebar), you can see the algorithm’s results updating.
- Keihin-Tohoku line has the highest score (top right).
- The direction is northbound (top right).
- The latest phase for each station is shown (middle right).
- When we reach the last
Locationin theSession, we can see the full Station history (middle right). - We can see the phase history for any station by clicking its current phase.
- When I click on a station, I can see on the map the
Locations that were used to calculate its phase.
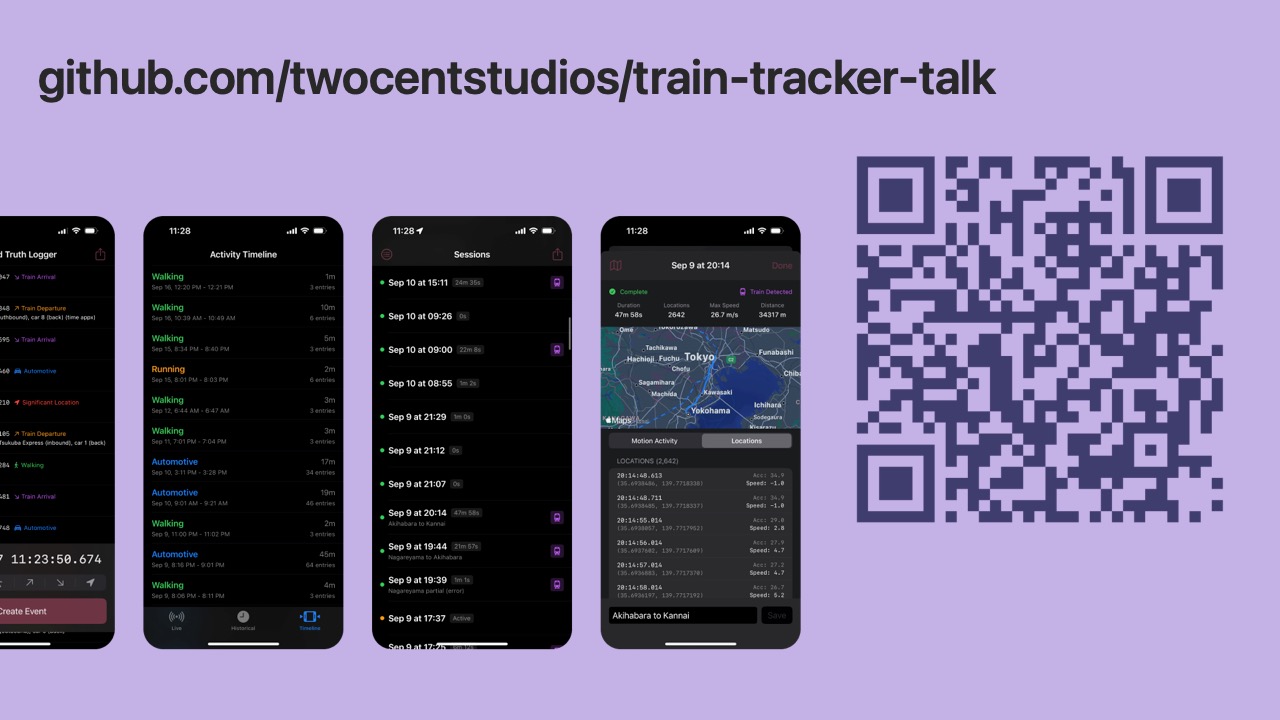
- The 5 iOS apps I created to collect this data are open source on GitHub.
- The macOS app and algorithm are included as well.

- The algorithm is still being improved!
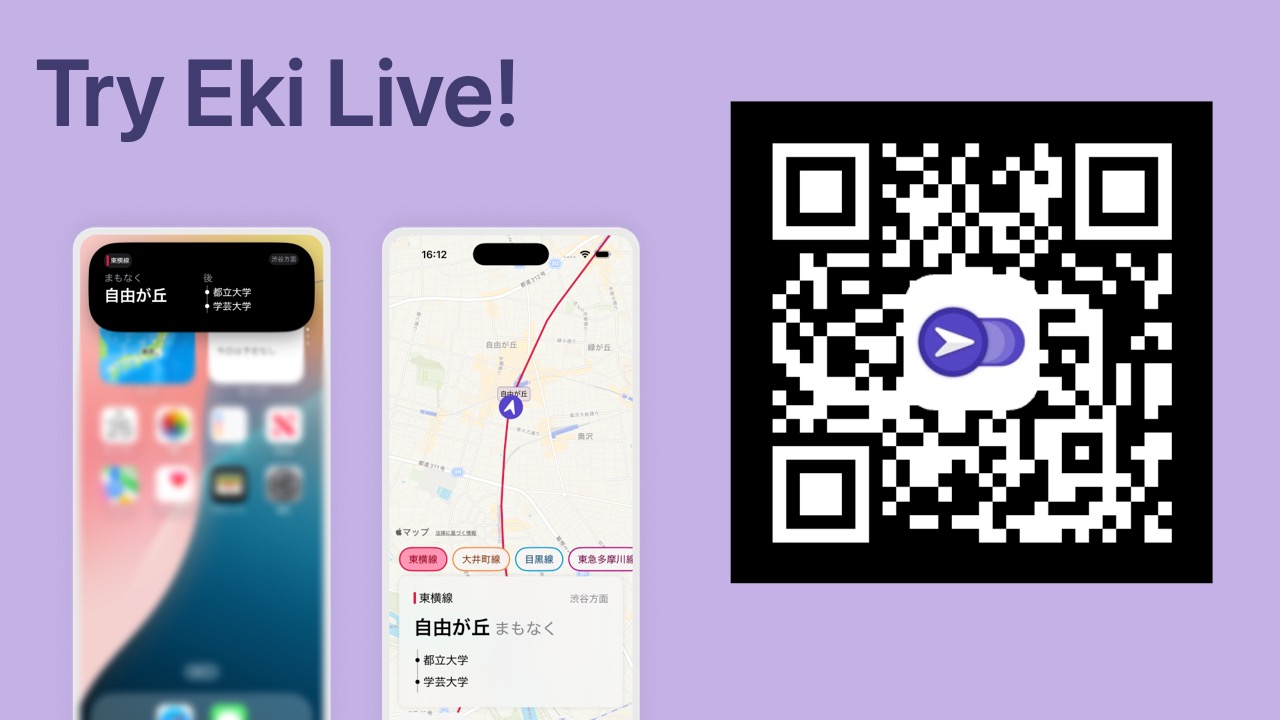
- But if you want to try it, Eki Live is on the App Store now.
- The app starts up automatically in the background and shows the next station in the Dynamic Island.

- Thanks for reading this presentation.
- If you have questions or comments, feel free to reach out.