Calculating the Area of Multiple Intersecting Rectangles with Swift
A piece of palate data I’m creating in my image to music generating app is the total ratio of the area faces in an image i.e. totalAreaOfFaces / totalAreaOfPhoto.
This turns out to be a lot like a classic programming algorithms interview question. Jump to Implementation if you want the TL;DR.
The code in this post targets iOS 9.3 and Swift 2.2.
Naive Solution
At first, this seems like a trivial problem. Apple provides us with a facial recognition algorithm in the CoreImage framework. This algorithm takes a CIImage as input and returns [CIFaceFeatures] each of which contains a bounds property. Take the area of each bounds and add them together then divide by the area of the image and we’re done.
/// WRONG - naive implementation
func ratioOfFaces(image: CIImage) -> CGFloat {
let context = CIContext(options: nil)
let detector = CIDetector(ofType: CIDetectorTypeFace, context: context, options: [CIDetectorAccuracy: CIDetectorAccuracyHigh])
let features = detector.featuresInImage(image, options: nil)
let faceArea = features
.map { $0.bounds }
.map { $0.width * $0.height }
.reduce(0, combine: +)
let photoArea = image.extent.width * image.extent.height
let ratio = faceArea / photoArea
let clampedRatio = min(ratio, 1)
return clampedRatio
}
The above implementation is fine if we assume that no face rects will intersect. Unfortunately, face rects can intersect. You can see this in the below image provided in the CoreImage documentation.

With the naive algorithm above, it’s possible for the output ratio to be greater than 1. For my purposes, it would be perfectly reasonable to use the above algorithm and clamp the output to 1, especially since an image that would produce a result greater than 1 would be very rare. There would have to be two or more faces that covered the entire area of the photo. However, I decided to see how complicated it would be to calculate the true combined area of an array of n overlapping rectangles.
Subtracting the Intersections
Before Googling, my first attempt at an algorithm went like this:
- Add up the areas of each rectangle in the input array.
- Exhaustively pair each rectangle in the input array with every other rectangle.
- Calculate the intersection rectangle between each pair.
- Subtract the intersecting rectangles from the total from (1).
This algorithm works if you can guarantee that only two (or an even number) rectangles can intersect. However, when three (or an odd number) rectangles intersect, the intersecting rectangle must be added back. It follows the inclusion-exclusion principle.
In visual form (thanks, Numbers):

3*3 + 3*3 - 3*1 = 15
green + red - (green && red)

(3*3 + 3*3 + 3*3) - (3*1 + 2*1 + 2*1) + (1*1) = 21
(green + red + black) - (green && red + green && black + red && black) + (green && red && black)
Notice the alternating + and -. Feel free to count them and see. If you don’t add back the 1*1 area covered by all three rectangles, your answer will be one short.
We’ve got to take it a step further.
Separating in One Dimension
More Googling led me to this algorithm. The pseudocode is as follows:
- Determine and sort the unique X values (minX and maxX) for all rectangles in the array.
- Split all rectangles whose area falls within X values from (1).
- Merge all rectangles (on the Y axis) that have the same minX (and maxX).
- Calculate the area of each rectangle from (3) and add them up.
Or in pictures:


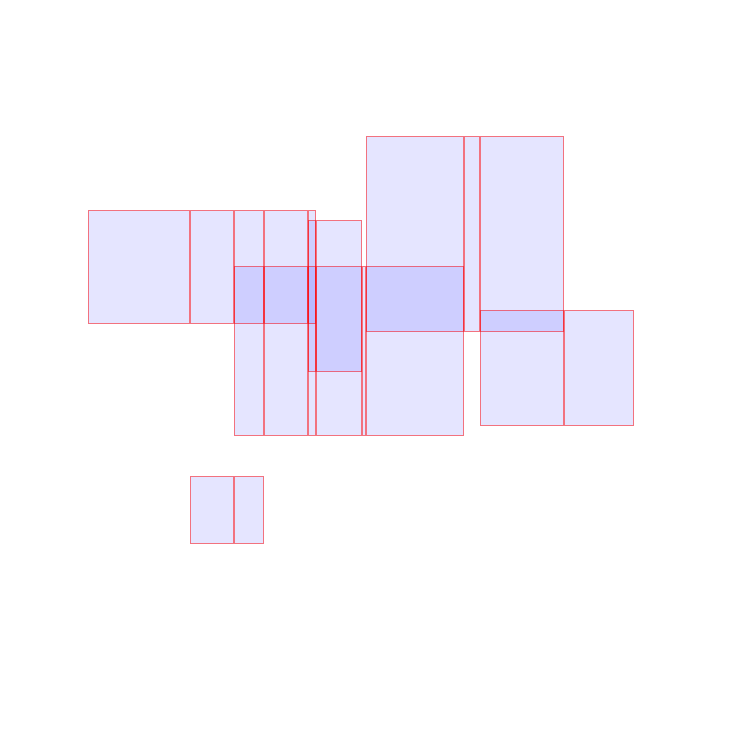
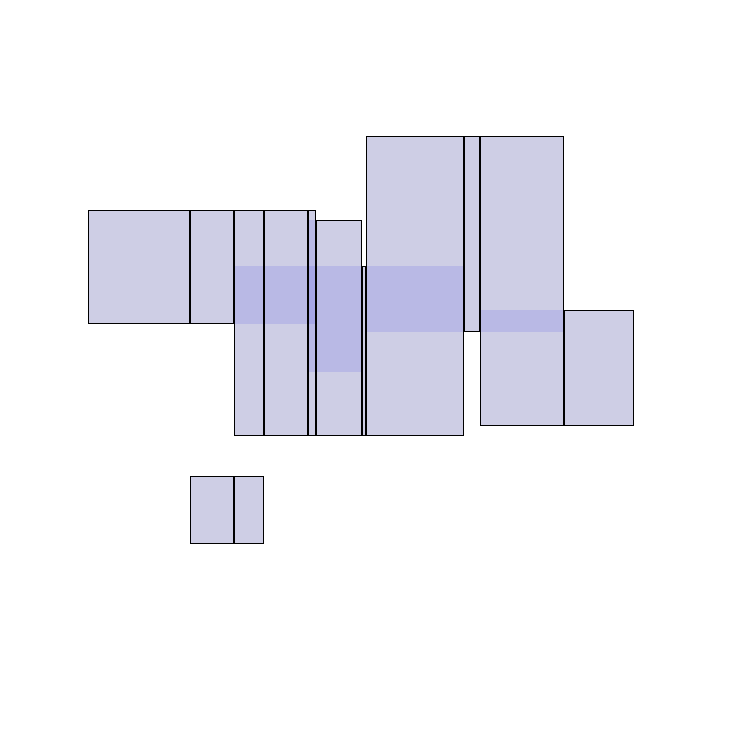
Implementation
We have five discreet steps and two helper functions to implement.
Note: I’m pretty fast and loose with mixing functional and imperatives bits.
Target Performance
Before we start, it’s best to pick a performance target for our use case so we don’t fall into the trap of preoptimizing. My best guess is that the 95 percentile case will have less than 5 faces detected in a photo. It’s possible, but very unlikely we’d have anywhere near say 1000 faces. Therefore, we don’t have to optimize performance very much. I’m going to target the algorithm on 5 faces taking less than 0.05 seconds.
High Level Function
func areaOfRects(rects: [CGRect]) -> CGFloat {
let nonZeroRects = rects.filter { $0.area != 0 }
let xDividers = uniqueSortedXDividers(nonZeroRects)
let splitRects = rectsSplitAtXDividers(nonZeroRects, xDividers: xDividers)
let combinedRects = combinedRectsOnY(splitRects, xDividers: xDividers)
let area = combinedRects.reduce(0) { (acc, rect) -> CGFloat in
return acc + rect.area
}
return area
}
The first step we have to add to the algorithm is to sanitize our input rect array for any zero area rectangles.
The middle three steps correspond to steps 1, 2, and 3 presented above.
The last step is to add up areas of all of our non intersecting rects to determine the final area.
Helper Functions
area
Area is pretty straightforward.
extension CGRect {
var area: CGFloat {
return self.width * self.height
}
}
splitAtX
We’ll also need a function to split any rect at an X value.
/// Split self into two rects at X. Otherwise, return self.
extension CGRect {
func splitAtX(x: CGFloat) -> [CGRect] {
if x <= self.minX || x >= self.maxX {
return [self]
}
let rect1 = CGRect(
x: self.minX,
y: self.minY,
width: x-self.minX,
height: self.height
)
let rect2 = CGRect(
x: x,
y: self.minY,
width: self.maxX-x,
height: self.height)
return [rect1, rect2]
}
}
CGRect already has a function CGRectDivide, but since we have to do specific bounds checking anyway, I found it easier just to write my own.
CGRectUnion
CGRectUnion(rect1, rect2) finds the smallest rectangle that contains rect1 and rect2.

CGRectIntersection & CGRectIntersectsRect
CGRectIntersection(rect1, rect2) finds a rectangle shared by both rect1 and rect2 or CGRectNull if they do not intersect. It has a boolean cousin called CGRectIntersectsRect.

uniqueSortedXDividers
Four transformations: take minX and maxX, flatten them back into one array, create a set to unique them, then sort min to max.
/// Collect and unique all X coordinates.
func uniqueSortedXDividers(rects: [CGRect]) -> [CGFloat] {
let xDividers = rects.map { [$0.minX, $0.maxX] }.flatten()
let xDividersUniqueSorted = Array(Set(xDividers)).sort()
return xDividersUniqueSorted
}
rectsSplitAtXDividers
For the outer loop, loop through each X value. For the inner loop, loop through each rect, split it if necessary, and return it to the array.
/// Split all rects at X coordinates.
/// Precondition: all rects must have non-zero area.
func rectsSplitAtXDividers(rects: [CGRect], xDividers: [CGFloat]) -> [CGRect] {
for r in rects { precondition(r.area > 0) }
var dividedRects: [CGRect] = rects
for xDivider in xDividers {
var running: [CGRect] = []
for rect in dividedRects {
let dividedInputRects = rect.splitAtX(xDivider)
running.appendContentsOf(dividedInputRects)
}
dividedRects = running
}
return dividedRects
}
combineRectsOnY
By splitting the rects on the X axis, we can now guarantee that:
- no rects will overlap on the X axis.
- all rects with the same minX will also have the same width.
Rects can still overlap on the Y axis though. We must now combine any rects that overlap.
Our outer loop is again on the X boundaries. The inner loop occurs only on the rects that lie on that X boundary, so we’re essentially touching each rect only once.
We have several conditions to handle for each X boundary.
- There are no rects that lie on the X boundary.
- There is one rect that lies on the X boundary.
- There are two intersecting rects that lie on the X boundary.
- There are two non-intersecting rects that lie on the X boundary.
- With more than two rects, any combination of 3 and 4.
Sorting rects by ascending Y value allows us to compare adjacent rects for intersection without skipping over any.
Within the sortedRects loop, we compare each rect to its preceding neighbor, combine them with CGRectUnion if they intersect, or add the previous rect to the output array if it does not intersect.
/// For each set of rects at an X boundary,
/// combine the intersecting rects.
///
/// Precondition: all rects on the same X boundary must
/// be equal in width.
static func combinedRectsOnY(rects: [CGRect], xDividers: [CGFloat]) -> [CGRect] {
var combinedRects: [CGRect] = []
for xDivider in xDividers {
let xFilteredRects = rects.filter { $0.minX == xDivider }
let sortedRects = xFilteredRects.sort { $0.minY < $1.minY }
guard let first = sortedRects.first, last = sortedRects.last else { continue }
if first == last {
combinedRects.append(first)
continue
}
var prev = first
for rect in sortedRects {
assert(rect.width == prev.width)
if CGRectIntersectsRect(rect, prev) {
prev = CGRectUnion(rect, prev)
} else {
combinedRects.append(prev)
prev = rect
}
}
combinedRects.append(prev)
}
return combinedRects
}
An alternate implementation of this step could instead divide all rects on the Y boundaries (similar to the second step of our algorithm), then discard any rects that are the same.
Using Our Function
Now that we can more accurately calculate the area of our face rectangles, here is the final implementation of our original problem.
func ratioOfFaces(image: CIImage) -> CGFloat {
let context = CIContext(options: nil)
let detector = CIDetector(ofType: CIDetectorTypeFace, context: context, options: [CIDetectorAccuracy: CIDetectorAccuracyHigh])
let features = detector.featuresInImage(image, options: nil)
let faceRects = features.map { $0.bounds }
let faceArea = areaOfRects(faceRects) // our algorithm
let photoArea = image.extent.width * image.extent.height
let ratio = faceArea / photoArea
return ratio
}
Other Algorithms
From my cursory research, I found at least two other unique algorithms.
The first is the brute force approach: create a matrix the size of the union of all rectangles (initialized to 0), “color in” the area of rectangles in the matrix with a 1, then count the number of 1s.
The second recursively finds intersecting rectangles and applies the aforementioned inclusion-exclusion principle to add and subtract the intersecting areas.
See the Reddit link in the References section below if you’re interested in reading more about these.
Conclusion
As an Electrical & Computer Engineering major in college, I didn’t get as much algorithms practice as you Comp Sci-ers, so this was a fun little exercise for me.
@ me on Twitter @twocentstudios if you have ideas for a better algorithm!