Deconstructing a chirp.io
UPDATE (10/13/12): The kind folks at chirp.io pointed me to their tech page. Read more at the end of the post.
TL;DR: I tried to figure out the chirp.io sound->URL protocol but failed.
I came across an interesting app today called chirp.io. From the chirp.io website:
Chirp is an incredible new way to share your stuff – using sound. Chirp sings information from one iPhone to another.
Just reading about it, I was very impressed. It’s not easy to encode a few hundred kilobytes of data (small jpeg) into a sound. But in the App Store blurb, it says:
Sharing requires a network connection.
Oh, so it’s actually just transmitting a link. Still pretty cool.
I downloaded the app and played a few of the example chirps. I noticed that they were relatively high pitched and seemed to be the same length. I also noticed they were monophonic - only one frequency was played at a time.
By tapping on a chirp, it shows what is basically a short URL for that resource. An example is chirp.io/gsm2h88c7u which links back to chirp.io/blog. You can also share images and text.
I did some similar DSP and frequency detection projects in college, so I decided to see if I could reverse engineer the protocol that chirp.io uses. I’m definitely no codebreaker or cryptographer, but we’ll see how far we can get.
Busting out the DAW
I usually use Magix Samplitude as my Digital Audio Workstation of choice, but since I was booted up on my OS X side, I decided to use cross-platform Reaper instead.
The first thing I needed to do was record the waveform. I could have direct connected into my sound card using a 3.5mm to 3.5mm jack, but I didn’t have one of those handy. I did have my Shure KSM27 set up, so I decided to record it through the air instead.
The first chirp I analyzed was chirp.io/gsm2h88c7u. If you notice, the short URL is only 10 characters long. We may be able assume that it uses lowercase characters a-z and 0-9.
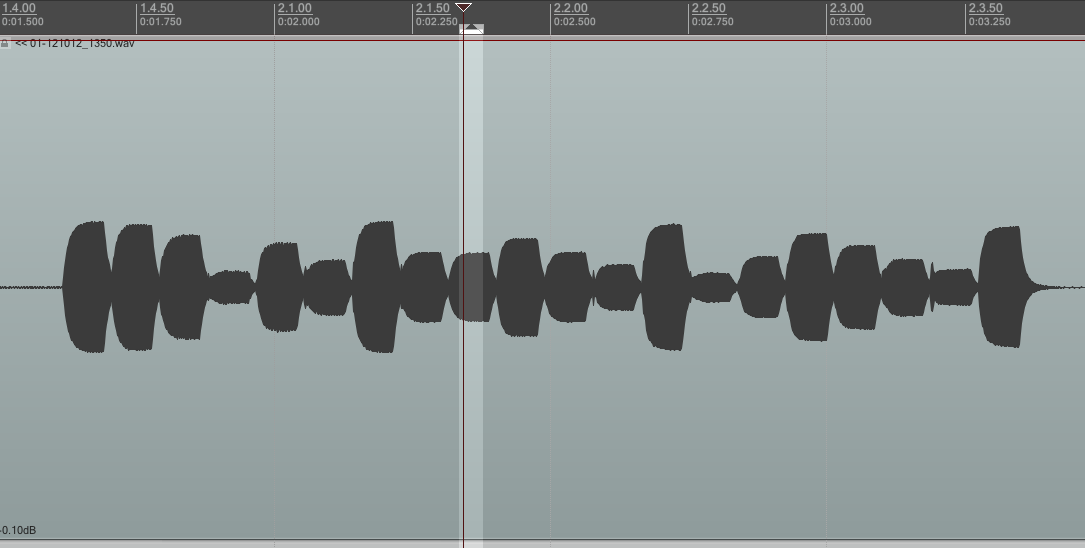
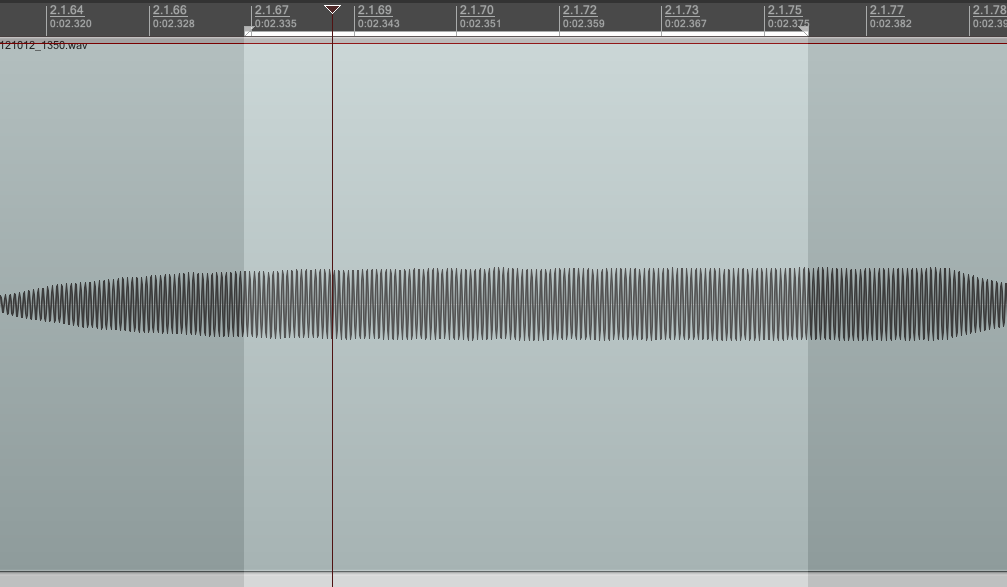
If you count, there are 20 monophonic segments in the chirp. Each segment is around 88ms long.
Reaper has a pitch detector plug-in, so I looped each segment and estimated the frequencies. The pitch detector plug-in sometimes got confused though, so I had to double check with a normal FFT.
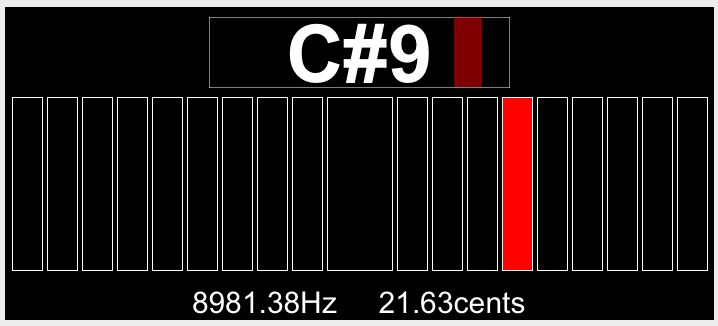
Looking at the data
I recorded the data for this first chirp:
chirp1 = [4717, 5300, 4453, 8981, 6324,
1976, 4717, 2797, 2797, 3522,
2640, 10000, 3737, 9400, 6660,
3965, 4189, 2220, 7131, 5613]
Those are the 20 frequencies in Hz in the order they’re played.
With only one data point so far, I decided to make an initial hypothesis:
- Points 8 and 9 are the same (2979Hz) so maybe that divides the chirp into a metadata section and a URL section.
- The unique URL part is 10 characters so maybe that’s sections 10-19 and 20 is the stop bit.
I can’t do much with only one data point, so I analyzed a second chirp. This one is a short text block with the URL chirp.io/mnac2dvevb.
chirp2 = [4717, 5300, 6324, 6660, 3143,
3522, 1976, 3737, 10844, 3965,
10844, 3329, 5000, 4717, 2797,
6660, 4189, 2098, 3965, 2220]
Hmm… not as much correlation as I expected. Let’s look at them side by side.
1 4717 4717
2 5300 5300
3 4453 6324
4 8981 6660
5 6324 3143
6 1976 3522
7 4717 1976
8 2797 3737
9 2797 10844
10 3522 3965
11 2640 10844
12 10000 3329
13 3737 5000
14 9400 4717
15 6660 2797
16 3965 6660
17 4189 4189
18 2220 2098
19 7131 3965
20 5613 2220
The only thing that stands out at first glance is segments 1 and 2 are the same. That would make sense as our start code.
Let’s combine these two sets, sort them, then discard the duplicates.
uniq_freqs = [1976, 2098, 2220, 2640, 2797,
3143, 3329, 3522, 3737, 3965,
4189, 4453, 4717, 5000, 5300,
5613, 6324, 6660, 7131, 8981,
9400, 10000, 10844]
Between the two chirps, there are 23 unique frequencies. So frequencies are shared quite a bit.
Now let’s subtract the neighbors to try to figure out how many we’re missing.
diff_freqs = [122, 122, 420, 157, 346,
186, 193, 215, 228, 224,
264, 264, 283, 300, 313,
711, 336, 471, 1850, 419,
600, 844]
I’d guess that we’re missing a couple from the low range, but a few more in the higher range. I expect the differences to increase as the we get higher up the scale, but that really depends on the frequency detection algorithm being used by the app.
It seems like we’re kind of stuck. My initial hypothesis is mostly wrong. It doesn’t look like frequencies map directly to letters. Let’s do one more chirp before we give up.
Flower Picture: chirp.io/9gf6q9ltu3
chirp3 = [4717, 5300, 2963, 4453, 4189,
2490, 7922, 2963, 5945, 9400,
10000, 2098, 7922, 5945, 7521,
3965, 8981, 5000, 4717, 2098]
1 4717 4717 4717
2 5300 5300 5300
3 4453 6324 2963
4 8981 6660 4453
5 6324 3143 4189
6 1976 3522 2490
7 4717 1976 7922
8 2797 3737 2963
9 2797 10844 5945
10 3522 3965 9400
11 2640 10844 10000
12 10000 3329 2098
13 3737 5000 7922
14 9400 4717 5945
15 6660 2797 7521
16 3965 6660 3965
17 4189 4189 8981
18 2220 2098 5000
19 7131 3965 4717
20 5613 2220 2098
uniq_freqs = [1976, 2098, 2220, 2490, 2640,
2797, 2963, 3143, 3329, 3522,
3737, 3965, 4189, 4453, 4717,
5000, 5300, 5613, 5945, 6324,
6660, 7131, 7521, 7922, 8981,
9400, 10000, 10844]
diff_freqs = [122, 122, 270, 150, 157,
166, 180, 186, 193, 215,
228, 224, 264, 264, 283,
300, 313, 332, 379, 336,
471, 390, 401, 1059, 419,
600, 844]
We’re now up to 28 unique frequencies. I’m not sure if there’s enough frequency space left to suggest they’re using a 36 character alphabet.
Unfortunately, it doesn’t look like we can deduce anything new from our third set of data. The two segment start code is the same. But other than that, there doesn’t seem to be any correlations I can tease out.
Analysis
My assumption that the unique URL component was related one to one with the frequencies was wrong. It’s looking more and more like there’s some sort of hashing combined with error detection/correction.
It looks like I’ve failed to deduce the protocol, but it’s interesting to see how chirp.io uses the frequency space.
I can’t find the specs of the iPhone internal speaker and mic, so I don’t know what the hard limits are for frequency response. But small speakers are bad at reproducing low frequencies so it makes sense that they’re not going lower than 1000Hz.
The upper limit is a little more difficult to determine. It still has to do with the limit of the speaker and mic, but at a certain point, those higher frequencies may start to get a little annoying, even if the duration is short. At a certain point, due to the limitations of human hearing, the higher tones wouldn’t be audible enough even if they were annoying. Chirps are supposed to sound like a continuous stream of notes, and therefore even if the mic could deduce the correct frequency, it would lose some of the value.
Another one of my initial assumptions was that the amplitude of each frequency segment was not relevant. From the waveform, it looked like all segments were not of equal amplitude, but that may have been due to micing the iPhone speaker, which basically puts another 3 filters on the signal (speaker response, air, and microphone response).
The App Store description also mentions that chirping works in noisy environments, so I’m going to stick with my assumption that even relative amplitudes aren’t used.
Looking at pitch detection algorithms, there are three choices: Time domain, frequency domain, or both.
A simple time domain algorithm like period detection through zero-crossing would not work in a noisy environment, especially for higher frequencies. Autocorrelation is possible especially since we are only looking for a single frequency. Frequency domain methods are also likely because the spacing between frequencies can be chosen and there are no harmonics to worry about.
The iPhone CPUs are powerful enough now to use almost any of the popular pitch tracking algorithms and libraries, so performance shouldn’t be a limiting factor.
Conclusion
I’m looking forward to trying out the chirp.io app with some friends to see how well it performs. It’s definitely a cool idea, and I’m interested to see if it picks up steam.
If you happened to have some insights about my data than I didn’t, it’d be great to hear about it: @twocentstudios.
Update
If I would have read the FAQ on chirp.io more carefully, I would have seen their post about the technology behind chirp.io.
I was almost there…
Let’s see where we went wrong.
- 20 pure tones - got that one.
- 87.2ms each - I estimated 88ms.
- 2 tone start code - got that.
- 32 character alphabet - I first guessed 36, but then revised to saying it probably wasn’t more than 30.
- [0-9, a-v] characters - I assumed they’d use up through ‘z’, and that it would start with letters and end with numbers.
- [startcode][shortcode][error-correction] - I’m not sure why I didn’t think the shortcode would be at the front.
- Pitch detection algorithm - nothing specific is mentioned yet, although the site says they’ll be publishing more on the topic soon.
- Error-correction with Reed-Solomon - I don’t have enough experience with error correction algorithms that I could have made a prediction on this one. But my lack of understanding did cause me to overestimate how good the pitch detection algorithm needs to be to recover the signal.
Error correction means that Chirp transmissions are resilient to noise. A code can be reconstituted when over 25% of it is missing or misheard.
Overall, it was a fun exercise and taught (or re-taught) me a little bit about DSP, coding & protocols, and I even got to play around with some Ruby.
I highly recommend downloading chirp.io if you’ve got an iOS device.